|
|
|
THE COLOR OF DEATH ROW
We are indebted to Rev. Jesse Jackson for inspiring a back-of-the-envelope calculation that evolved into this essay. When La Griffe du Lion opened the cover of Jackson's book, Legal Lynching: Racism, Injustice and the Death Penalty, we recognized immediately the hand of illogic and bombast we have come to expect. When Jackson submits that, "African Americans make up 25 percent of Alabama's population, yet of Alabama's 117 death row inmates, 43 percent are black," we know that not even he accepts this tired argument as evidence of racial discrimination. It is quintessential Jackson, offering pabulum to his public. Death row cannot be a racial mirror of America, because blacks commit murder at a higher rate than whites - seven to eight times higher. Yet, the simplicity of Jackson's racial-mirror argument is appealing. Cleaned up to account for differential homicide rates, it becomes a powerful tool for assessing bias. This we have done and will now elaborate. Along the path to death row, race can insinuate itself at any point, from the prosecutor's decision to seek the death penalty, to the jury's verdict (recall O.J.) or recommendation of a death sentence. Of course, we could argue that sex or appearance might exert similar influences, and we would probably be correct. Chasing discrimination at every turn is burdensome and loaded with statistical pitfalls. Variables are many - controlling them a challenge. Even the choice of dependent variable may not be obvious. That is why we are indebted to Rev. Jackson. His racial-mirror argument considers none of this. It cuts to the bottom line: the color of death row. It disregards detail, seeing only the sum of bias on the road to execution. It is an "integral" approach, and asks only one question: Given black and white homicide rates, is death row too black, too white or just right? Uncorrected for differential murder rates, the answer is: too black. Corrected, the answers vary and may sometimes surprise. The Color of Death Row without Bias
Table 1 shows us that patterns of violent behavior resulting in death are vastly different for whites and blacks. The differences are essential to a correct interpretation of death-row statistics. First notice that blacks kill mostly blacks, whites kill mostly whites, white-on-black murder is negligibly small, and most important for our purpose, the per capita murder rate for blacks is about 7.4 times that of whites. That is, A black is more than 7 times as likely to commit murder as a white. From these and similar data, we can model death row as it would exist in a bias-free justice system. Its racial complexion will serve as a benchmark. Suppose, in a given state, there are a total of N black and white inmates on death row. The probability, Pn , that n are black is given by the binomial distribution,
where pB and pW are the probabilities that a random inmate is black or white, respectively. We have isolated a black and white universe so that pB + pW = 1. Equation (1) is a yardstick for measuring racial equity. It describes death row as it would exist in a racially-neutral justice system. We can use it to find the probability of a particular racial mix on death row. More useful is the probability that the number of blacks (or whites) falls within a specific range. We obtain this by summing (1) over that range. Thus, the probability, Pab , that the number of blacks on death row falls in the interval [a , b] is
Another useful quantity is the most probable number of blacks on death row. This is the value of n that yields the largest Pn in (1). Because the binomial distribution is fairly symmetric, the most probable number of blacks (an integer) is very close to the average number of blacks (a non-integer). The average number of blacks is pB N. For the cases we consider, we can without error take the most probable number of blacks to be pB N rounded to the nearest integer. We cannot proceed much further without a value for pB , the probability that a randomly selected inmate is black. This probability varies from state to state depending on the population mix. States with few blacks will have fewer blacks on death row. Rev. Jackson would argue that pB is the black population fraction of the state, but of course that is not so. The probability, pB , is the black fraction of capital murderers, a vastly different number. For convenience, assume that the black fraction of capital murderers is equal to that of other murderers. Let NBM be the number of black murderers and NWM the number of white murderers in a given state. Then for that state,
We define the per capita black to white murder-rate ratio, R ,
where NB and NW are the black and white populations, respectively, in the state. Evidence suggests that criminal behavior and consequently R , is more characteristic of race than of geography. In fact, data show R to be essentially invariant to crossing state boundaries, its value falling between 7 and 8. That is, a black is between 7 and 8 times more likely than a white to be a murderer. The quantity, R, may be evaluated from population and crime databases. Because the per capita black to white murder-rate ratio, R , is nearly constant,
we find it convenient to express pB in terms of it. From (3)
and (4) we write
Though R remains constant, the population ratio, NW / NB , varies by state. In Figure 1, using a value of 7.5 for R, we see how the probability of a random death-row inmate being black varies with a state's population mix. 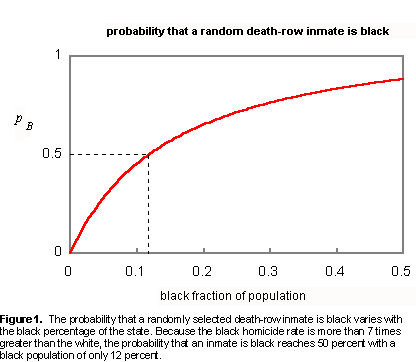
As of April 1, 2000, Alabama held under sentence of death 97 whites and 86 blacks. Following Rev. Jackson, we observe that African Americans are 26 percent of Alabama's population, but 47 percent of death row. (Our numbers are more recent and thus differ a bit from Jackson's. The newer data are even more objectionable from his vantage.) But is Alabama's death row really too black as Jackson alleges? Using in (5) a value of 7.5 for the black to white per capita homicide ratio, R, we find the probability, pB , of a random death-row inmate in Alabama being black to be 0.729. That is, "on average" we should find 72.9 percent of Alabama's death row to be black. If the Alabama justice system were bias free, the most probable number of blacks in its 183 prisoner death-row would be (0.729)(183) or 133. With only 86 blacks under sentence of death, Alabama's death row is too white -- much too white! How unlikely is Alabama's death row? Statistical fluctuations normally produce clustering about most probable values. In statistical terms, the best question to ask is how many standard deviations (SD) from the most probable number of blacks (133) is the actual number (86)? The standard deviation, σ, of a binomial distribution is given by
For Alabama, N = 183 and pB = 0.729, yielding σ = 6.01. Thus the number of blacks on death row is (133-86)/6.01 or 7.8 SD away from the most probable number (133). The likelihood of finding this number of blacks (or fewer) on death row by chance is 1 in ~1014. Not only do we find the sentence of death in Alabama to be biased against white suspects, it is extraordinarily so. We subjected each state, with a death penalty, to similar analysis. In some states a small black population precluded a meaningful statistical analysis. (For example, only 1 in ~1700 Idahoans is black.) Still other states have death rows too small or with too few blacks to obtain useful results. For those states meeting the statistical requirements, we summarize our findings in Tables 2, 3 and 4.
Bias and Geography An unexpected geographic pattern of bias emerged from the calculations. States biased against white suspects cluster in the South, and stretch west into Texas. Moving north, a band of race-neutral states materializes. Only one state, Pennsylvania, is biased against black suspects. The pattern of bias is mapped in Figure 2. 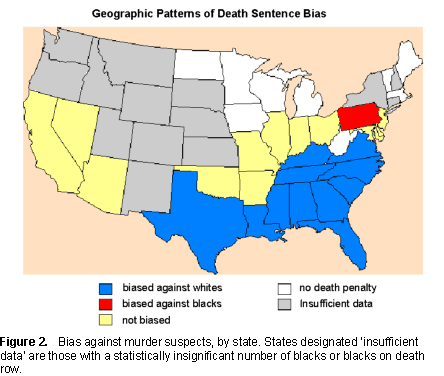 Death-Row Details Our "integral" approach to death-row bias revealed it and also located it geographically. To learn more, we must turn to "differential" studies, which operate conventionally by throwing hundreds of variables into a regression engine. Of this genre, the most cited study (and perhaps the best) is by University of Iowa law professor, David Baldus. Baldus with his colleagues conducted a massive statistical investigation of capital cases in Georgia in the seventies. By controlling an extensive list of variables including aggravating factors, race of the murderer and victim, number of victims, jury composition and more, they demonstrated (at least in Georgia) that the race of the victim, much more than that of the accused, influences the outcome of capital cases. Specifically, they found that a murder suspect is most likely to be charged with capital murder if his victim is white. He is also more likely to receive a death sentence for killing a white. The suspect's race is minimally important. Simply put, white victims are "valued" more than black victims in Georgia. Evidence suggests this is true elsewhere in the South. How then did we find a pattern of discrimination against white suspects? Do our results conflict with those of Baldus et al? Not at all. They are perfectly compatible. Because whites mostly kill whites and blacks mostly kill blacks, if white victims are valued more, white perpetrators will be more likely to get a death sentence and end up on death row. We might say that white suspects pay the price for discriminating against black victims. The eminent sociologist, Steven Goldberg, observes that eliminating discrimination against black victims would have the paradoxical effect of increasing the percentage of black murderers sentenced to death.
And from the ACLU:
The NAACP and ACLU are working from the same script. It is a script used by many death-penalty opponents, because they all take their cues from the same source: the Supreme Court ruling in McCleskey v. Kemp (1987). Justice Powell wrote for the majority:
But the Court made a boo boo. After so many years, death-penalty opponents should know that the Supreme Court confused odds with probability. (For more about this, see Arnold Barnett's delightful article, How Numbers Deceive.) Baldus found that the odds (not the probability) of receiving a death sentence were 4.3 times greater for a defendant charged with killing a white than for killing a black. Odds are defined as probability divided by (1 minus probability). If you do the arithmetic, you will find that the probability of a death sentence for killing a white victim, PWV , is not 4.3 times the probability, PBV , for killing a black. The two probabilities are related as follows:
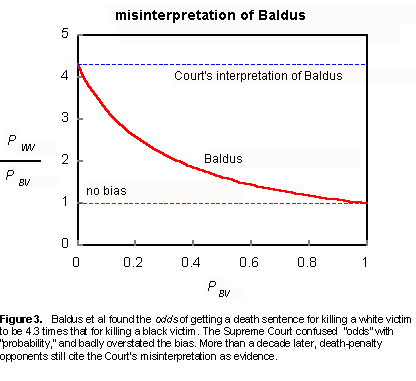 From Figure 3 we see that the probability of receiving a death sentence for killing a white victim was greatly exaggerated by the
Court. Only when the chance of a death sentence is very small (i.e., not many aggravating circumstances) is the factor of 4.3
approached. But since the death penalty is not likely to be imposed under these circumstances,
the victim's race becomes moot. None of this is to say that the victim's race is unimportant. In the gray area where the death penalty is neither very likely nor very
unlikely, it is a factor, not as big as the Court supposed,
but enough to account for the bias observed in the
South. There is no need for the NAACP, ACLU and others to build on the Court's
error. ### |
"Given black and white homicide rates, is death row too black, too white or just right?"
"Death row cannot be a racial mirror of America, because blacks commit murder at a higher rate than whites."
"With only 86 blacks under sentence of death, Alabama's death row is too white."
"States biased against white suspects cluster in the South and stretch into Texas."
"The Supreme Court confused odds with probability."
"The NAACP and ACLU continue to trumpet the Court's false conclusion."
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||