Only the most committed egalitarian ideologue can deny the black edge in basketball, football and sprinting. Tune in an NBA game and there is a fair chance you will find ten black players on the court. Try an NFL game. Most of the faces on the field will be black as well. Then measure this against the fact that blacks comprise about 13 percent of all Americans. But nowhere is black superiority more dramatically illustrated than in sprinting. No white has ever run a 100m in less than 10 seconds. At least 30 blacks have. 

   The simplest explanation (usually the best) for black dominance in these sports is innate talent. Measurable anatomical and physiological differences support this conclusion. However, this interpretation being offensive to multicultural sensibilities, remains unpopular. We will avoid the issue. Our aim is to make the black-white ability gap precise, not to ponder its origins. 

   Throughout this essay, the term "black" means people of West African ancestry. In America they are mostly descendants of slaves brought here from regions we now call West Africa. They differ both in body type and range of athletic abilities from other black African peoples. The term, "white" refers to Europeans or people of European descent. 

   Reggie White took some heat for his remarks. Perhaps he would have had better luck if he used sports to illustrate racial differences. Consider a simple case: Japanese baseball teams are not competitive with American teams. The foreigners who play in Japan routinely lead the leagues in hitting. The reason can be traced to the discovery of a young cub who collected baseball cards. On the front of each card was a picture of a major leaguer. The back of the card contained some statistics like the player's career batting average, home run production, stolen bases and so on. Also listed were the player's height and weight. The cub soon noticed major league baseball players were significantly taller than average Americans. Their heights also tended to cluster in a narrow range. Almost all were over six feet, but not many were extra-tall basketball types. It occurred to the cub there might be an ideal height for baseball players, big enough for power but not big enough to present a huge strike zone. He surmised that Japanese baseball teams were second-rate not for lack of zeal or athleticism. They simply did not measure up. 
 

WHICH SPORTS TO STUDY? 
   A big-league sport is about winning. On the athletic battlefield meritocracy is king. Athletes fill slots in rank order of ability. There is no room for affirmative action. The ingredients needed to quantify the black-white ability gap are all there: meritocratic selection, strong motivation and lots of candidates competing for a few slots. 

   Winning demands meritocratic selection. Politics on the playing field and winning do not mix. Motivation is provided by breathtaking financial rewards that await those who make the big time. Not many with the potential to make the NFL or NBA could afford to abandon the pursuit of such a career while any hope remained. At this writing, average annual salaries are $2.6 million in the NBA, $900,000 in the NFL, and $1.7 million in major league baseball. The rewards of track and field do not match the salaries of the big three team sports, but in the marquee events the best athletes earn very well. A mixture of shoe endorsements, appearance fees and prize money can easily total more than $1 million for top performers. Finally, in a country of almost 300 million, only a few thousand athletes will strike it rich. 

   Sports best suited to our analysis rely on a few basic physical attributes. Football is too complex. In no other sport is division of labor more evident. A football team is a collection of specialists, with an enormously broad range of athletic ability represented among its players. The running backs combine speed with explosive power. (In the NFL they are all black.) Wide receivers are fast, agile and jump like gazelles. (They are almost all black.) On the offensive line conservation of momentum rules. Bulk and strength get the job done. Three hundred pounds of humanity does not yield easily. And because there is no black monopoly on bulk or strength, we find whites on the front line. Place kickers, punters, line backers, punt returners and more round out a team. Each position brings with it its own physical demands. The assortment of physical requirements that football requires provides powerful testimony to the general athleticism of blacks, who make up about two-thirds of the NFL rosters. 

   Race and ethnicity are confused in Major League Baseball by sports statisticians who classify blacks as Hispanic when they are obviously just blacks with Hispanic surnames. In spite of the large black presence in baseball, it does not lend itself well to our study. The large proportion of Latin American players of unclear race presents a problem. 

   Basketball skills are few and elemental. Quickness, jumping ability, eye-hand coordination and size form the basic arsenal of good basketball players. These qualities can be developed only so far (size not at all) before running up against genetic constraints. Basketball will be well suited to our analysis. 

   Perhaps, of all athletic competitions, the purest and most dependent on natural gifts is running. It is a primal survival ability, whose simplicity makes it especially suited to our purpose. It is also universal. Show me a man who has not known the thrill of a sprint and I will show you a man born without two good legs. On every block, in every town the fastest kid is soon discovered. 

   With strong dependence on simple endowments, basketball and sprinting are well suited to our study. It is no coincidence both are dominated by athletes of West African ancestry. Data from each sport will enable us to assess the black-white gap. 
 

GAMES WE CAN PLAY 
   After precisely defining and measuring the gap, we will be able to answer all manner of questions. Here are a few. (The reader will no-doubt come up with more.) 

• What is the probability that a randomly selected adult American white male will be faster than his similarly selected African-American counterpart? 

• Suppose an integrated suburban high school with, say, 2000 students. If the school is 25 percent black and 75 percent white, what is the most likely racial composition of the basketball team's starting five? 

• It is possible to increase the NBA's white representation by increasing the number of teams in the league. How big would the NBA need be to make it half white? 

• What is the most probable a priori racial composition of the Dream Team that will represent the USA in the 2000 Olympics? (At this writing the Dream Team has already been selected.)

THE ATHLETIC QUOTIENT, AQ  
   Few areas of human activity are documented with as much detail as major-league sports. On its website, the NBA provides daily updates of player stats. They are sortable on various statistics like total points, rebounds per game and much more. With the NBA season about a third over in late December 1999, we selected 150 of the NBA's finest to grind up in our engine. We chose the 150 players who were averaging the most points per game, limiting our selection to Americans who had played in at least 10 games. They were not all stars, but neither was any a scrub. Of these players, 135 were black and 15 white. We will translate these numbers into a more general measure of black superiority. 

   Let us assume the existence of a quantity that measures the collection of attributes that enables an athlete to perform in his sport. We call it the athletic quotient or AQ. It will not be necessary to define AQ precisely, only to specify a few of its properties. Each sport has its own set of physical demands, so that AQ is not a universal measure of athletic ability, but rather a specific measure for a specific sport. Good sprinters are generally not good swimmers. Blacks with their high body density have to work just to stay afloat. Thus, we can expect some racial/ethnic groups to have high AQs in one sport and low AQs in others. Black domination of basketball and sprinting suggests that the AQ for these sports may be closely related. We shall see. 

   We assume that the distribution of AQ in the black and white populations are of the same form but displaced from one another along the AQ axis by the quantity Δ. (Standard units are used throughout.) That is, if P_B(x) is the probability distribution of AQ for blacks, and P_W(x) that for whites, then P_W(x) = P_B(x+Δ). The quantity, Δ, is the black-white AQ gap. 

Basketball AQ.  Consider the pool of NBA aspirants to be all American men between the ages of 20 and 35. From this pool no more than 348 will make the NBA active list at any one time. 

   Let f_B and f_W be the fractions of blacks and whites, respectively, with AQ greater than or equal to some value, λ. (For example, λ might be the AQ needed to get into the circle of 150 players who put the most points per game on the board.) These fractions are given by 

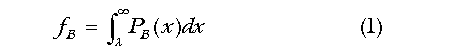and 
 

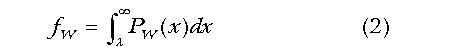
   We note the following transformation: 
 

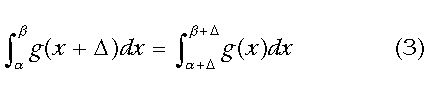and write for f_W, 
 

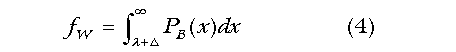   What value of the gap, Δ, will account for the racial composition of the 150 NBA high scorers? We first find the threshold AQ, λ, that selects them out. The number of blacks who made the cutoff (135) divided by the number of blacks in the pool of aspirants, is the quantity, f_B. The Census Bureau estimates 4.12 million black men between the ages of 20 and 35 in the U.S. in 1996. Using this value to compute f_B, and assuming P_B is Gaussian, (1) may be solved numerically for λ, with the result: λ = 4.0 SD. That is, the threshold for this inner circle of 150 NBA players is about 4 SD from the mean of the black population at large. This is very rarefied territory indeed. The fraction of whites, f_W, who make the cutoff is the number of whites (15) divided by the 25.7 million white men between 20 and 35 estimated by the Census Bureau. Using this value of f_W, and the value of 4.0 for λ, (4) may be solved numerically for Δ, yielding Δ = 0.87 SD. That is, the black-white basketball AQ gap is 0.87 SD. A white must have a minimum AQ almost 5 SD above the white mean to make the inner circle of 150 NBA top scorers. 

   If we were to look at the circle of 150 again a week or a month later, we would likely find its composition to be different from the 135/15 black-white breakdown we found one day in late December. Each look could produce a different value for Δ. We want to establish a range where we would expect to find Δ most of the time. The number of blacks in the circle of 150 is a binomial variable. Its variance is given by np(1-p), where n is the number of players (150) and p is the probability of a player being black. Estimating p as 135/150, the variance of the sampling error is 13.5 and the corresponding standard error is 3.67. The central limit theorem tells us that the sampling distribution of blacks (or whites) that we find in our various surveys will be approximately normal. Consequently, the 95% confidence interval for the number of blacks in the circle of 150 is 135 ± (1.96)(3.67). From the extremes of this interval we can map a 95% confidence interval for the gap, Δ. Doing so, we find that repeated sampling of the circle of 150 should produce values of Δ that 95% of the time will fall in the interval [0.78, 1.01] with a most probable value of 0.87. 
 

Sprinting AQ.  Running is a solitary undertaking, which lends it a certain nobility. The best athletes compete against the clock as much as against other runners, and the available data reflect this uncommon aspect of the sport. We focus on the apotheosis of speed: the 100-meter dash. The record holder in this event is known as the world's fastest man. On Peter Larsson's website, http://www.algonet.se/~pela2, we found a remarkable compilation of the 819 all-time best 100m performances from October 1964 to September 1999. There were 111 runners on the list, many having contributed more than one of the best performances. Fifteen of the 111 were native West Africans. Most of them were relative newcomers, 14 of the 15 making the list in the last five years. 

   We can speculate why native West Africans are latecomers to the ranks of the very best sprinters. West Africa has a combined population of 200 million. Seven of its 19 nations have illiteracy rates over 70% and six others over 60%. Côte d'Ivoire, the richest country in the West Africa, has a per capita income of about $850. In such an environment, overlooking concealed talent is easy. In the U.S., high-school coaches are quick to spot athletic promise. In West Africa many boys never even make it to high school. West Africans and African Americans have entirely different access to athletic opportunity. In fact, it is remarkable that of the 111 all-time best 100m runners, 15 were West African. It is even more remarkable when we note that native West Africans comprise only about 1/30 of the world's population. Their recent emergence among the ranks of the world's best sprinters reflects improved opportunity. Still, if we seek a black-white (more properly a West African-European) AQ gap for sprinting, comparing groups with historically similar access to the big time is best, especially since the data stretch back to 1964. Accordingly, we eliminated native Africans from the list of 111. We also removed two Japanese, leaving us with 94 runners, 80 of West African descent and 14 of European descent. 

   The fractions of blacks and whites, f_B and f_W, needed to compute Δ, were estimated by assuming a world population containing 1 billion whites of European descent and 100 million in the West African Diaspora. Twelve percent of these were assumed to be between the ages of 20 and 35. The calculation yielded a most probable AQ gap for sprinting of 0.82 with a 95% confidence interval of [0.72, 0.96]. Table 1 summarizes the estimated black-white gaps for both basketball and sprinting. 
 

Population sample	Most probable Δ (SD)	95% confidence interval (SD)
NBA high scorers	0.87	[0.78, 1.01]
Top sprinters (no Africans)	0.82	[0.72, 0.96]
Table 1.   Black-white AQ gaps for basketball and sprinting.

 

   The AQ gap values for basketball and sprinting are conspicuously close. Their 95% confidence intervals span almost the same part of gap space. Coincidence? We doubt it, but cannot prove it either way. Both sports rely heavily on fundamental physical attributes. Jumping ability, prized in the NBA, is not in the sprinter's bag of tricks. But the same powerful legs and fast-twitch muscles that drive a man forward can also propel him upward. In the NFL blacks dominate the ranks of wide receivers and corner backs, where both speed and leaping talent are valued. The case that AQ for basketball and sprinting stems from a common set of physical attributes bestowed more abundantly upon blacks is circumstantial but strong. 
 

PLAYING WITH THE GAP 
   We turn now to the questions posed previously. We asked for the probability that a young adult white American will be faster than his African American counterpart, both being selected randomly. The question reduces to finding the probability that the white has a higher sprinting AQ. The probability that the black has an AQ between y and y + dy is P_B(y)dy. Let g(y) be the probability that the white has an AQ > y. That is, 
 

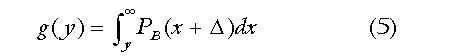   The conditional probability that the white has the higher AQ given that the black has an AQ between y and y + dy is g(y)P_B(y)dy. Integration over all values of y gives the probability, p, that the white has the higher AQ. That is, 
 

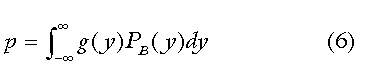   Using Δ = 0.82 in (6) returns the value 0.28 as the probability that the white is faster. Thus, a random white has a reasonable chance of out-sprinting a random black. However, as competition gets stiffer, athletes move into the high-end tail of the AQ distribution, where whites are badly outnumbered. 

   Next we looked at a hypothetical integrated high school with 2000 students, 25 percent black and 75 percent white. We asked for the most likely racial composition of the starting five on the basketball team. Assuming half the students are male, we will fill 5 slots in rank order of basketball AQ from a pool of 750 whites and 250 blacks. Being a bit more general, suppose N_S slots are to be filled in order of AQ from a pool of N_B blacks and N_W whites. All those with an AQ equal to or greater than some value, λ, will be selected. The pool sizes, N_B and N_W, the number of available slots, N_S, and the AQ gap, Δ, determine the cutoff AQ. The variables are related as follows: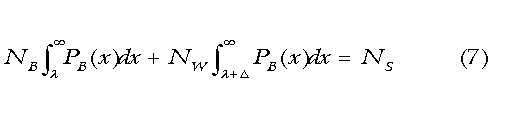 

   The first term on the left side of (7) represents the number of blacks who make the cutoff; the second term is the corresponding number of whites. The two terms add up to the number of slots, N_S. The cutoff AQ, λ, is obtained by solving (7) numerically. We then evaluate each term the left side of (7) to get the number of blacks and whites who make the cutoff. For the case at hand, N_B = 250, N_W = 750, and N_S = 5. For Δ we used the value 0.87 SD obtained from the analysis of the NBA data, and found λ = 2.14 SD. That is, the cutoff AQ is 2.14 SD above the black mean. The first term on the left of (7) evaluates to 4.03, the second to 0.97. Consequently, the most probable makeup of the starting five would be 4 blacks and 1 white. If we perform the same analysis for a half white school of the same size, the starting five would most probably be all black. 

   The next question asked to what size the NBA would need grow to make it half white? The question may be rephrased as: What value of N_S will make the 2 terms on the left-hand side of (7) equal to each other? Doing the arithmetic, we find the NBA would have to grow to approximately 860,000 and field almost 72,000 twelve-man teams to obtain a league half white and half black. 

   Finally, we asked for the most probable racial makeup of the Olympic Dream Team. This is like the high school starting five question with different input. The pools, N_B and N_W, are the respective numbers of black and white American men between the ages of 20 and 35. The number of slots, N_S is 12. Again using the basketball AQ gap of 0.87 we found the most probable Dream Team would have 11 blacks and 1 white. The team selected in January 2000 had precisely this composition. It is worth noting that all the Dream Teamers were high up on the list of 150 high scorers used to assess the gap. We also note that the lone white on the team ranked last among his teammates on this list. 
 

   We hope that readers will use the techniques developed here to explore other aspects of human biodiversity. If you do, please share your insights with La Griffe du Lion.