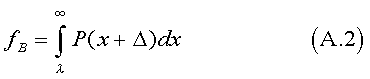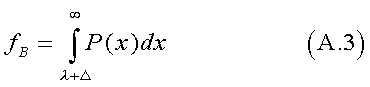|
|
THE EFFECT OF URBAN
FLIGHT
ON IQ DISTRIBUTION
A violation of the fundamental law of sociology is
unearthed, pointing the way to an appraisal of inner-city and suburban IQs, and
the characterization of cognitive discontinuities caused by urban migratory
patterns.
|
There are very few moments in a man's existence when he experiences so much hostility, or meets with so little
benevolence, as when he challenges fashionable perceptions of race.
-- La Griffe du Lion, 2002
The fundamental law of sociology
If,
as he begins this essay,
the reader finds himself unacquainted with the fundamental law of sociology, he should not
be reproached, for the law is first about to be articulated. It is a difficult task
that we undertake, though in fact it is undemanding and straightforward. It is
difficult because those who will welcome our results eagerly are among the most
perfidious of our species, while those who reject them will do so out of antipathy
not discernment. Sandwiched between the devil and the fuzzy-minded are the learned and sagacious readers of La
Griffe du Lion, to whom we address our remarks.
The fundamental law of sociology is a summary of hundreds of
observations. It asserts that:
On large-scale
tests of reasoning ability, the observed mean difference between non-Hispanic whites and African Americans is 1.1 +
0.2 standard deviation.
The observation is so unerringly reproducible, it justly earns the appellation, law.
Appropriately, we call 1.1 SD the fundamental constant
of sociology. Table 1 illustrates.
Table 1.
The Fundamental Law of Sociology Illustrated |
|
B/W Mean
Difference (SD) |
|
|
| 0.99 |
Math SAT, U.S. average 1998 |
| 1.11 |
NY bar exam first attempts 1985 - 1988 |
| 1.13 |
National bar exam first attempts of every U.S. law student
first enrolled in fall 1991 |
| 1.19 |
1986, 1987, 1988 results of National Board of Medical
Examiners Exam Part I (required of all U.S. medical
students) |
| 1.21 |
Armed Forces Qualifications Test (from National
Longitudinal Survey of Youth) |
The anomaly
There being no more reliable indicator of racial cognitive differences than the standardized math exam, we were
surprised recently by a puzzling anomaly -- an apparent violation of the fundamental law.
Anomalies are sometimes swept aside because, after all, they are just anomalies.
Sometimes, however, they fit into another design not immediately apparent, in
which they are not aberrations, but rather the norm. So it was with this
exception. The irregularity turned up on Maryland's usually reliable standardized 8th grade math test, part of the Maryland School Performance Assessment Program (MSPAP).
Like many standardized-exam programs, MSPAP is a huge repository of cognitive
information waiting to be extracted. Each May, all Maryland public school 3rd, 5th and 8th
graders take these tests. Results are reported in exceptional detail, fully disaggregated by race and ethnicity, and reported down to the level of
individual school.
While browsing MSPAP pass rates looking for patterns, we happened upon something
extraordinary -- a black-white math gap of 0.55 SD, half that
predicted by the fundamental law. The anomaly showed up in data from Baltimore,
Maryland's largest city. Almost seven-thousand Baltimore 8th graders contributed
to this result, a sample too big to write off as a statistical aberration.
There was, of course, the
chance that pass rates were erroneously reported, so we went back and looked at
results from each of the last nine administrations of this test (1993 to 2001).
Over nine years we found an average gap of 0.61 + 0.07 SD. The
anomaly was confirmed!
We had found a
reproducible violation of the fundamental law.
The irregularity was confined to Baltimore. Statewide, the
gap on the same test over nine years was a remarkably constant 1.11 +
0.05 SD, in perfect accord with the fundamental law. What had Baltimore done to
so reduce the racial gap? It was not education reform or inspired
pedagogy that cut the gap. It was demography.
Urban migration in the twentieth century
When John and Mack Rust invented the first reliable cotton picking machine in 1936, they could not have imagined the
sociological impact it was to have. Perfected in the 1940s, the machine could pick as much as fifty men at one-eighth the
cost. It gradually replaced Southern, mostly black field hands. Out of work, they turned northward to earn a living. Three-quarters of the 6.5 million blacks who migrated north between 1910 and 1970 left
the South after the cotton picking machine came
into widespread use. Jim Crow may have started the great migration, but it was the emergence of this new technology that
fueled it.
Black migrants settled mostly in Northern and Midwestern cities where they found work in low-skilled jobs. Barred from
most residential areas, their neighborhoods hardened into overcrowded crime-plagued ghettos. Whites, facing an
inhospitable intrusion into their lives, began a migration of their own to more remote parts of the city and eventually to the
suburbs.
With the passage of civil rights legislation in 1964, new residential opportunities opened for blacks. They began their own
urban exodus, following whites to the suburbs. By the end of the twentieth century, most whites with the means to leave
the central city had already done so. Black flight, however, was alive and well.
Starting from near zero in 1960, by 1990 32 percent of metro-area blacks lived
in suburbia, 39 percent by 2000.
But escape from the inner city is a highly selective
enterprise. It is an option open mostly to the right half of the bell curve.
Consequently, urban flight creates a cognitive discontinuity where the city
meets the suburbs. Left behind in the city is a human residue wanting in
human capital. Unemployment, welfare dependency, drug addiction, coarseness and
incivility are its hallmarks, low IQ its nub. Below we characterize the
discontinuity, closely estimating mean IQs of inner-city and suburban dwellers, black and white.
Methodology
In December 2000, La Griffe du Lion introduced the method of thresholds.
Designed to assess group differences
in "fuzzy," i.e., poorly-defined, variables like aggressiveness, criminality and sex drive, the method works as well for
precisely defined variables like IQ. Though the calculations are performed analytically
(Appendix A) we will take a
graphical walk-through to reveal their underpinnings as we assess the mean IQ of African Americans in
Maryland.
The method of thresholds employs surrogate variables. Here,
we use MSPAP test scores as a stand-in for IQ. Input is the
proportion of each of two groups that attains a "satisfactory" score, i.e.,
reaches the threshold. (MSPAP pass rates
are reported at two levels of performance, "satisfactory" and "excellent." )
Over nine years and roughly half a million test scores, 58.8% of white and 19.1% of black 8th graders passed at the
satisfactory level. Figure 1 shows the white test score distribution, assumed Gaussian. (See
Appendix B for a justification
of the use of Gaussian functions.) The distribution is normalized to make the area under the curve unity. The passing
score is marked on the score axis (abscissa) as "satisfactory pass." It is placed to make the area under the curve
to the right of it (shaded in the figure)
equal to 0.588, the white passing fraction.
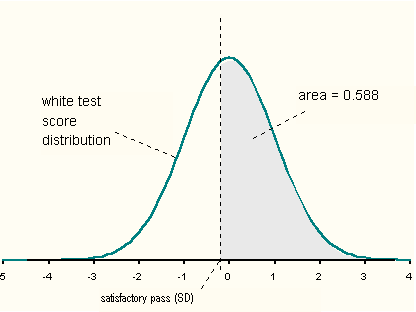 Figure 1.
Normalized distribution of MSPAP math scores for white 8th graders statewide. The
satisfactory-level passing score is located so as to make the shaded area equal
to the passing fraction, 0.588. Figure 1.
Normalized distribution of MSPAP math scores for white 8th graders statewide. The
satisfactory-level passing score is located so as to make the shaded area equal
to the passing fraction, 0.588.
Next we locate the black distribution on the same axes (Figure 2). This is accomplished by shifting the (white) distribution
left until the area under the curve to the right of the passing score equals the
black passing fraction, 0.191. The mean
difference is the distance separating the two curves, measured here to be 1.1 SD. 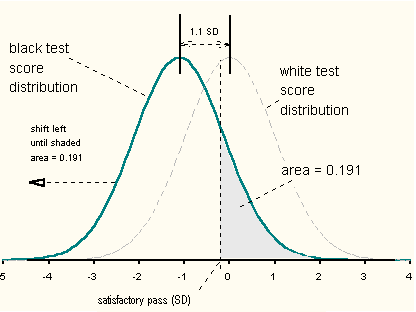 Figure 2.
Without changing the passing score, shift the white distribution left until the area under the curve to the right of
the passing score equals 0.191, the black passing fraction. The black-white mean difference is the distance separating the
two curves. Figure 2.
Without changing the passing score, shift the white distribution left until the area under the curve to the right of
the passing score equals 0.191, the black passing fraction. The black-white mean difference is the distance separating the
two curves.
Conversion to IQ units is straightforward. Customarily, the mean IQ of non-Hispanic whites is set to 100, with a standard
deviation of 15. A gap of 1.1 SD then corresponds to a mean black IQ in Maryland of 83.5, i.e., 100 - (1.1)(15).
The method of thresholds, as illustrated above, yields a statewide black-white cognitive gap of 1.1 SD, in
agreement with the fundamental law. To dispel any suspicion of fortuity, we divided the data into nine independent parts
corresponding to the nine administrations of the test between 1993 and 2001. Each year's data was analyzed separately.
Table 2 shows the result of this computation. The average of the nine values was 1.106 SD with a standard error of 0.045, ruling out
fortuity.
Table 2.
Statewide Black and White Satisfactory-Level
Pass Rates and Gaps
MSPAP Eighth-grade Math |
|
| year |
pass rate (%)
black |
pass rate (%)
white |
B/W gap
(SD) |
|
1993
1994
1995
1996
1997
1998
1999
2000
2001 |
11.4
15.3
19.0
17.2
19.5
21.3
22.2
24.7
21.5 |
48.2
53.1
54.8
57.8
60.7
61.8
64.5
65.3
62.6 |
1.160
1.101
0.999
1.143
1.131
1.096
1.137
1.077
1.110 |
|
| average gap = 1.106 + 0.045 |
Effects of urban flight on IQ distribution
Maryland's big city, Baltimore, saw its population peak just short of a
million in 1950. It has been declining for nearly half a
century, 17% in the last twenty years alone. Today it numbers about 651,000.
White flight followed by black has drained the city of inhabitants. As its population
dwindled, Baltimore like many other Northern and Midwestern cities without
significant recent foreign immigration became blacker. Today, Baltimore is 65%
African American, and 32% non-Hispanic white.
Baltimoreans who fled the city moved mostly to neighboring Baltimore County. The County,
which surrounds the city, is the first stop on the way out. Thirty years ago Baltimore County was lily white. Today, African Americans
are 17
percent of its 726,000 inhabitants. And they keep coming.
Table 3 illustrates the effect that urban flight has had on IQ
distribution. We computed mean differences between Maryland's non-Hispanic
white population and each of four local groups: inner-city and suburban blacks
and whites. From these, we computed mean IQs, assigning a value of 100 to
Maryland's non-Hispanic white population with a standard deviation of 15. (Affluent whites and blacks inside the city are not represented
in these data. They neither live
in slums nor send their kids to public schools.)
Table 3
Mean Differences (SD) with Respect to Maryland Non-Hispanic Whites
Corresponding Mean IQs
|
|
| year |
Baltimore City
blacks |
Baltimore County
blacks |
Baltimore City
whites |
Baltimore County
whites |
|
1993
1994
1995
1996
1997
1998
1999
2000
2001 |
1.68
1.51
1.38
1.72
1.69
1.54
1.62
1.52
1.47 |
0.945
0.847
0.886
1.031
0.975
0.865
1.018
0.918
0.949 |
1.120
0.909
0.808
0.956
0.984
0.962
1.015
0.979
0.916 |
0.048
0.063
0.068
0.058
-0.010
0.070
0.106
0.019
-0.019 |
|
| avg |
1.57 + 0.11 |
0.937 + 0.061 |
0.961 + 0.080 |
0.045 + 0.038 |
|
| IQ |
76 |
86 |
86 |
99 |
Conclusions
Baltimore is typical of many Midwestern and Northern cities, whose demographics were forever changed by the great black
migration of the twentieth century. Not unexpectedly we found a cognitive discontinuity at the city line.
Surprising, however, was its magnitude. Whereas suburban mean IQs (86 for
blacks, 99 for whites) conform more or less to national norms, city IQs are dreadfully low.
With a mean IQ of 76, inner-city blacks fall about 0.6 SD below the African American
average nationally. More than a third have death-penalty immunity on grounds of
mental retardation. The inner-city white mean of 86 is nearly a full standard deviation below the national white
average. By this measure, whites fared worse than blacks. Both groups are seriously deficient in human capital. Neither
is very employable. To compound matters, we almost certainly have overstated urban IQs. City residents constitute a low-IQ group extracted from a more cognitively representative population. Their kids, whose test scores we
analyzed, should have regressed toward their racial means, i.e., toward higher IQs. That is,
inner city kids are smarter than their
parents. Accordingly, our estimates of inner-city IQs are best regarded as upper bounds to adult values.
IQ hardens early in life, locking in the urban deficit. With
few prospects for improvement, cities must
look elsewhere for amelioration. While we all are aware of the advantages that accrue to the brightest among us,
we
also know that other qualities carry with them inestimable benefits. Traits like honesty, reliability,
perseverance and self-discipline, when cultivated contribute to employability and to a more productive life in general.
Indeed, for low-skilled jobs these latter qualities are more important than intellect. Unfortunately,
casual observation finds such virtues also wanting.
Finally, we note that a problem cannot be solved until it is defined. This we have done. But where we see cognitive
inadequacy, some will find only abject, hopeless misery. As for our efforts, we can be certain of only one thing --
vilification. It could drive a man to pseudonymity
###
APPENDIX A. THE
METHOD OF THRESHOLDS
Let PA(x) and PB(x) be the normalized probability distributions of the group property, x, measured in units of standard
deviation, for members of group A and B, respectively. The distribution functions for the two groups are assumed related
by the translation, PB(x) = PA(x + Δ).
Let fA be the fraction of A's who reach or surpass some threshold value of x, say λ. That is,

The fraction, fB, of B's who reach or surpass λ is:
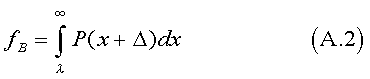
where Δ is the mean difference, <xA> - <xB>.
Equation A.2 is conveniently transformed as follows:
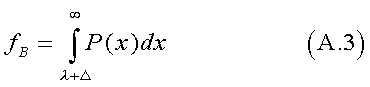
From the known fractions, fA and fB ,
both the mean difference, Δ,
and threshold, λ, may be obtained by simultaneous
solution of (A.1) and (A.3). Reader Ken Hirsch shows how,
using Gaussian distribution functions, this may be simply
accomplished with a spreadsheet. (Appendix B justifies the
use of Gaussians in the analysis of MSPAP data.)
###
APPENDIX B.
A NOTE ON THE USE OF GAUSSIAN DISTRIBUTION
FUNCTIONS
To apply the method of thresholds, we assumed Gaussian test-score distributions. A word justifying their use is in order.
MSPAP provides two passing-score thresholds, "satisfactory" and "excellent," which fall on widely separated parts of the
score axis. If Gaussians apply, the two thresholds should, within reasonable bounds, yield the same value
for the mean difference.
Above, we computed statewide black-white mean differences from satisfactory-level pass rates. We
repeated the calculation for each of nine years, this time using excellent-level pass rates. Table B.1 shows
the result. The average gap was 1.136 SD + 0.053
compared to 1.106 + 0.045 obtained from satisfactory-level thresholds. Within the
standard errors indicated, the two thresholds yield the same gap, validating the use of Gaussians in this context.
Table B.1
Statewide Black and White Excellent-Level
Pass Rates and Gaps
MSPAP Eighth-grade Math |
|
| year |
pass rate (%)
black |
pass rate (%)
white |
B/W gap
(SD) |
|
1993
1994
1995
1996
1997
1998
1999
2000
2001 |
0.260
0.463
0.868
0.942
1.29
1.80
2.56
2.93
2.41 |
5.94
7.42
8.96
11.7
13.0
16.6
22.1
21.7
19.4 |
1.23
1.16
1.04
1.16
1.10
1.13
1.18
1.11
1.11 |
|
| average gap = 1.136 + 0.053 |
|
|
|