|
How to Optimize Productivity with a Multiracial Workforce:
The Theory of Differential
Cutoff
The casual reader, inclined toward meritocratic ideals, may be put off by what follows, wherein a hypothetical wager between two college
presidents evolves into a method for optimizing productivity. But be assured that the
procedure developed herein adheres strictly to the principles
our reader holds dear.
|
After reviewing all the irrelevant evidence, we conclude that the virtues of diversity are
manifest.
-- La Griffe du Lion, 2003.
Mentor. Welcome Prodigy. On time as usual.
Prodigy. Good morning, Mentor, I so look forward to our meetings.
Mentor. I am happy to see you too Prodigy. Perhaps we can make some headway
today with the problem I left you with at our last visit. I sent it
to colleagues worldwide, but have not yet received a satisfactory solution. Here,
let me refresh your memory with the problem I call "Estati's Wager."
You have agreed to head a University admissions committee in return for the
president's support of your candidacy for the the Dirac chair. Lorenzo Estati,
the incoming president, has bet the outgoing president that the first freshman
class under his tenure will obtain the highest GPA ever. As chairman of the
admissions committee you are charged with winning Estati's wager.
Eschewing affirmative action, Estati instructs your committee to fill the
freshman class with the most capable applicants. As usual, applicants for
freshman seats represent various races and ethnic groups. How do you select the class
to maximize the chances of winning Estati's wager?
Prodigy. Actually, Mentor, I have produced a general solution.
Mentor. Oh my, you must tell me more ... One minute, that must be Professor Brasse at the door. I invited him to
join our discussion of the Estati Wager.
Welcome Marcel, come in. I want you to meet my young friend, Prodigy. Prodigy, this is Marcel Brasse of the
Department of Psychology at Sandbag University. Professor Brasse, as you may know, is a world renowned expert in
belongingness.
Prodigy. It is an honor to meet you, Professor. Accounts of your latest theory have appeared in every major print medium
as well as TV and radio. Fascinating stuff. I am eager to hear about it firsthand.
Brasse. You must be referring to my theory of minority underperformance.
Prodigy. Exactly.
Brasse. You know, then, that my colleagues and I have discovered the reason for minority underperformance. Mentor
thought my expertise in this area might help solve a problem he e-mailed to me.
Mentor. Prodigy has seen the problem, Marcel. I planned for us to discuss it today. But first, Marcel, perhaps you would
take a minute to give us a thumbnail summary of your theory and tell us how it might bear upon the Estati Wager.
Brasse. You know how I love to talk about my work. We at Sandbag have demonstrated that self-doubt and disquietude
prevent minorities from performing up to their ability. The problem originates with white people and their perception of
minorities. Whites tend to pigeonhole minorities, categorizing them as poor performers. After a lifetime of exposure to
these demeaning and false perceptions, minorities themselves begin to accept them as
fact, engendering feelings of inadequacy.
Ordinary circumstances become menacing. In class or when confronted by an examination, minorities become so jittery
they perform one standard deviation below other groups. I call the effect pigeonhole menace.
Prodigy. Professor, what distinguishes pigeonhole menace from other explanations of minority underperformance like
racism, poverty, the legacy of slavery, a culture of anti-intellectualism, distrust of whites, high
illegitimacy rates, etc.?
Brasse. Unlike other theories, the pigeonhole menace school (PMS) is founded on evidence. I do experiments. When, for
example, I include a check box for race at the top of an examination, African American students solve fewer problems than
when I don't.
Prodigy. Do all minority students react this way?
Brasse. No, some are more pigeonhole-menaced than others. Many, if fact, do just fine. We are currently conducting twin
studies now to see if susceptibility to pigeonhole menace is heritable.
Mentor. I would love to hear more, Marcel, but we are straying a bit from the topic. Have you had a chance to think about
the Estati Wager? I thought your singular expertise could provide some insight.
Brasse. I have looked at your problem, Mentor, so warm up the Dirac Chair. It is a no-brainer.
Prodigy. I can hardly wait.
Brasse. Don't let this out of the room, but we know that the predictive validity of the SAT is high. When combined with
high school grades it is dynamite. In fact, after applying corrections, correlation (validity) coefficients higher than 0.7 have
been reported. Thus, to win the Estati Wager, simply admit students in rank order of
their scores on a composite of SAT and
high school GPA. Of course, personally, I would never be associated with an admissions process that excluded pigeonhole-menaced African Americans.
Mentor. What are the corrections you mentioned, Marcel?
Brasse. Validity studies examine the relationship between test scores and performance, but they do this only for admitted
students. Rejected candidates do not get a chance to contribute to the data. This skewing results in
low estimates of the
correlation. In college admissions the range of scores going into the mix is further restricted because schools and applicants
mutually select each other. Fortunately, mathematical techniques are available that correct for this restriction of range.
Other difficulties include the fact that courses and major fields vary in difficulty. To some extent each of these effects can
be corrected. In a massive study of 48,000 students from 45 institutions, using a combination of SAT and high school
record as the "test," Ramist et al (College Board Report Number 93-1; ETS RR-94-27) reported corrected validity
coefficients as high as 0.76.
Prodigy. Wow, with that kind of detail at your fingertips, I see why you get $300 an hour for expert testimony.
Brasse. Remember now, none of this leaves the room. Don't think me disingenuous, but in my professional capacity as
"expert witness" I apply two rules, the Brasse canons of successful testimony: 1) Always refer to the variance or square of
the validity coefficient. It is so much smaller; and 2) Ignore meta-analyses like that of Ramist et al that report validity
coefficients 0.7 or higher.
Mentor. What do you think, Prodigy? Will rank order selection on SATs plus high school grades win the Estati Wager?
Prodigy. It would seem plausible that rank ordering on the best predictor would find the best candidates, but as
you know, things are not always what they seem. If the applicant pool is multiracial or multiethnic, rank order selection
will not maximize student productivity or any other productivity. A freshman class selected
in this way will almost certainly not obtain the highest GPA.
Brasse. Prodigy, if you could demonstrate
the fallibility of standardized tests, you will have my full support. I aim to rid the world of
them.
Prodigy. You had better hold off until I explain. It is not standardized testing that is at fault, it is rank ordering.
Brasse. I think I know what you are saying, Prodigy. Could it be that pigeonhole-menaced applicants will test under their
ability and consequently be screened out by rank order selection?
Prodigy. Not exactly, Professor. In truth, standardized tests overpredict job
and school performance for minorities.
Consequently the tests work to their advantage.
Mentor. How big is the overprediction?
Prodigy. Humongous. Robert Klitgaard, in his book Choosing Elites, provides some data. Based on his experience with
admissions at Harvard, Professor Klitgaard says you need to subtract 240 points from the combined verbal and math SAT
scores of blacks to have unbiased prediction for blacks compared to whites.
Mentor. Do you recall a paper a few years back, by (I believe) Edward Miller. Just a minute while I check my files. I don't
have your total recall, Marcel. Ah, here it is: The Relevance of Group Membership for Personnel Selection: A
Demonstration using Bayes' Theorem, Journal of Social, Political, and Economic Studies, Vol. 19 (Fall 1994) No. 3,
323-359. In his paper Miller demonstrates that to obtain comparable performance, higher test scores
are required of
those belonging to low-scoring groups, sort of a reverse affirmative action.
You know if taking a course were more pigeonhole menacing than taking a test, Klitgaard's observations and Miller's
proof would be consistent with pigeonhole menace theory.
Brasse. Yes! If different circumstances produce different degrees of pigeonhole menace, all is explained. This is a major
refinement, Mentor! I shall call it variable pigeonhole menace. We could write it up together.
Mentor. You are very kind Marcel, but I don't have time for the media attention a new Brasse theory would generate.
Nevertheless, I do appreciate your very generous offer. Now, Prodigy, can you show us how to assure Estati a win.
Prodigy. My solution to the Estati Wager uses standardized tests, but permits applying different cutoff scores to each racial
or ethnic group à la Miller. An applicant will be admitted if his test score equals or exceeds the cutoff score for his group.
Otherwise, he will be rejected.
Specifically with respect to Estati, cutoffs would be selected to produce the highest freshman GPA. I prefer, however, to be
more general and use terms like output or productivity rather than GPA. College admissions, after all, may be regarded as
just a special case of hiring. My solution applies more broadly. It is a blueprint for maximizing widget production,
identifying the most trainable recruits, or admitting a freshman class. I call it differential cutoff theory, or DCT for short.
Mentor. If your methods were adopted, the world would have to accept the principle of reverse affirmative action, in which
whites and Asians would get preferential treatment.
Prodigy. I see that only as a minor problem. Colleges and businesses already use affirmative action in admissions and
hiring. They would simply have to redesignate which groups are preferred. Perhaps you could give DCT a boost, Professor.
A few words from Marcel Brasse would carry immense weight with the media. I am sure that 60 Minutes or Nightline
would be eager to have us on together. And your next popularization of pigeonhole menace in The Arctic Monthly could
include a section on DCT. With you as a sponsor it would only be a matter of time before reverse affirmative action
became the law of the land.
Brasse. I don't think the world is ready for you, Prodigy. In fact, I don't think I am ready for you. Besides, you have not
yet explained your theory.
Prodigy. I'm sorry, let me elaborate. Suppose we have some slots to fill with applicants who belong to various ethnic or
racial groups. The groups differ in ability. Each applicant takes a "test." (So long as the result is put on a numerical scale,
even a simple interview could serve as a test.) If a candidate's score equals or betters his group's cutoff score, we hire or
admit him. DCT finds the cutoff scores that will put together the most productive workforce.
Brasse. How do you measure productivity,
Prodigy?
Prodigy. For admissions, freshman GPA is usually taken to be the criterion of performance, because
freshman courses are
less varied. Measures of employee performance are more diverse. The rate of widget production, or total cash receipts
across a checkout counter are but two examples. Each business has its own way to evaluate
employees.
For the Estati Wager per se we want to choose the group cutoffs that maximize freshman GPA. Let me illustrate
with a sketch. 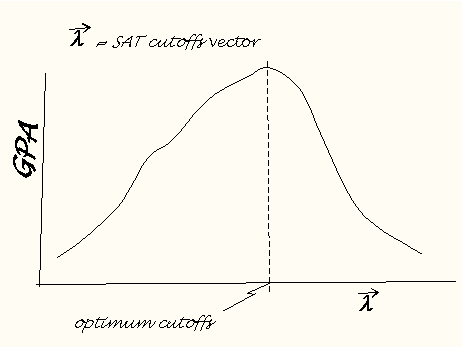 The abscissa is a symbolic axis representing all possible sets of cutoffs. DCT simply locates the point on the cutoff axis
that corresponds to the maximum GPA. The abscissa is a symbolic axis representing all possible sets of cutoffs. DCT simply locates the point on the cutoff axis
that corresponds to the maximum GPA.
Mentor. Are units a problem? GPA is on a four-point scale, while SAT scores vary from 200 to 800.
Prodigy. Converting to standard units, that is, units of standard deviation from the mean, eliminates that problem. In
standard units, both predictor and performance are measured with the same ruler.
Mentor. Before you get to the details, can you tell us what lies behind differential cutoff theory?
Prodigy. In a word, luck.
Brasse. Luck?
Prodigy. Yes, as in most human endeavors luck plays a role. Applicants who test high by good fortune are unlikely to
perform up to expectation on the job. If
the lucky high scorers could somehow repeat their tests de novo, most would
do worse.
Members of low-scoring groups are more likely to have filled slots by luck than members of higher-scoring groups. Upon
retest, therefore, the mean score of a low-scoring group would be depressed more than
that of a higher-scoring group. In a sense, job or class performance is a retest. Consequently, performance will suffer most among low-scoring
group members. It's Klitgaard all over again. You know the effect as "regression to the mean."
Basse. Yes, of course.
Mentor. But Prodigy please.
Precisely how do you win the Estati Wager?
Prodigy. OK, here it is. To win the Estati Wager or more generally to select the highest performing group of
candidates from a multiracial or multiethnic applicant pool, choose the group cutoffs (λ's) to satisfy
these relations.
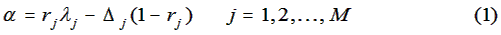
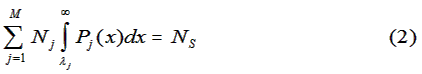
In these equations:
M is the number of racial or ethnic groups in the applicant pool.
NS is the number of slots to be filled.
For group k:
rk is the validity coefficient.
Δk is the mean test score difference between
k-group members at large
and
whites (whites minus group k).
Pk(x)dx is the probability that a member of group k scores between
x and x + dx, and
Nk is the number of group k applicants.
The quantity, α, is an undetermined function of the system parameters including validity coefficients, group mean
differences, the number of candidates from each group, and the number of available slots.
The M + 1 relations (1) and (2) uniquely determine the values of α and the M cutoff scores (λ1,
..., λM) that maximize
productivity.
I don't want to tire you, Mentor, so I included the proof and full development in an
appendix. Please excuse its didactic
style as I expect to present DCT to my friend Paul's 7th grade class.
Mentor. What do you use for the distribution functions, Pk?
Prodigy. DCT will
accommodate any distribution, but for most cases Gaussians are suitable. Many tests such as the General Aptitude Test Battery
(GATB), SATs, and
IQ tests have approximately normal distributions, which differ for various racial and ethnic groups by a translation.
Brasse. I think PMS will persevere over DCT on grounds of parsimony. Nevertheless, I am curious. Could you illustrate
with an example how differential cutoff theory works?
Prodigy. OK. Suppose you want to set up a widget factory. You have several options including where to locate your
factory and how to hire a workforce. You will need about 300 workers for jobs that require low to middle-level skills
typical of factory work.
You know that the best predictors of performance for many types of job are cognitive tests, so you plan to screen
applicants with one of the best, the General Aptitude Test Battery (GATB) developed by the US Department of Labor.
Chapter 3 of The Bell Curve, published too early to include a treatment of DCT, includes an otherwise terrific discussion of
the benefits of cognitive testing. I'll use its conservative estimate of 0.4 for the validity coefficient of the GATB for routine
jobs like widget fabrication and assembly.
Brasse. The Bell Curve was published at a time that pigeonhole menace was still an embryonic idea. I wonder how
Herrnstein and Murray would have treated PMS.
Mentor. I hope kindly, Marcel. Please continue Prodigy.
Prodigy. You have narrowed where to locate the widget factory to three cities. Each is populated primarily by whites and
African Americans. City A is 70 % black, B is 50 % black, and C is 10 % black. Otherwise the cities are equally attractive,
with good access to labor and transportation.
Suppose in each city 2000 applicants apply for a widget making job. Their racial makeup is in proportion to that of the
city. Of these, 300 will be selected. Let's compare for each city the expected rate of widget production if 1) we hire by rank
order on GATB scores and 2) we apply differential cutoff theory to the GATB scores. I've summarized the results in a
table, assuming a 1.0 standard deviation black-white cognitive gap.
Productivity: DCT vs. Rank Ordering
|
| City |
%
Black |
Black
Applicants |
White
Applicants |
Mean
Productivity*
(Rank Ordering
on cognitive
ability) |
Mean
Productivity*
(by DCT) |
productivity
Increase
using DCT |
|
| A |
70 |
1400 |
600 |
0.205 |
0.323 |
57.3 % |
| B |
50 |
1000 |
1000 |
0.399 |
0.464 |
16.3 % |
| C |
10 |
200 |
1800 |
0.592 |
0.600 |
1.2 % |
* Productivity is measured in standard deviations above the white population mean.
|
Mentor. I notice that DCT's advantage depends on the racial composition of the applicant pool. Can you comment on that?
Prodigy. Differential cutoff theory is most useful when the workforce is largely minority, a circumstance characteristic of
many cities. As the minority population becomes small, DCT asymptotically approaches rank order selection. DCT's benefits also depend on the labor supply. Generally, DCT's advantages show up better in a tight labor
supply. If in City A, for example, with its 70 % black population, we had 1000 instead of 2000 applicants for the 300 jobs,
the percent productivity increase effected by DCT over rank ordering would grow from 57.3 % to 273 %. Each
employment situation needs to be evaluated individually. An inescapable conclusion, however, is that maximum
productivity can always be achieved best by locating in a low-minority region.
Mentor. Where can we find how to do these calculations?
Prodigy. DCT is fully developed in the appendix. Its implementation will be greatly facilitated by processing software like
Mathematica, Maple, or Matlab.
Brasse. Is there a downside to differential cutoff theory?
Prodigy. Well, sure. Fewer minorities will be hired.. Given a particular supply-demand picture, DCT adjusts the racial mix
of a workforce to optimize productivity. That is sure to result in a reduction in the number of minorities hired.
Mentor. How serious is the reduction?
Prodigy. Judge for yourself. Using rank order selection in City B with its 50-50 black-white population split, 48 of the 300
widget-making jobs would go to blacks. Optimizing productivity with DCT would cut that number to 1.
Closer to the Estati Wager, let's look at 1997 enrollment data from the University of Texas Law School following the
Hopwood decision. Have you heard of La Griffe du Lion?
Brasse. The racist coward?
Prodigy. La Griffe analyzed enrollment data from the Law School at the University of Texas following the Hopwood
decision in March 1996. Here is what he said in The Color of Meritocracy.
La Griffe was pleased to find a bright spot, however transient, in the diversity wars. The University of Texas at Austin is
one of our nations's best. Before 1997, its Law School practiced race norming in its admissions process. White and Asian
students formed one pool of applicants admitted from test scores and grades. Blacks and Mexican Americans formed
another pool. They were considered separately and admitted on the basis of other factors, including race and ethnicity.
Cheryl Hopwood changed all that. She is a white woman who successfully challenged the University of Texas Law
School's admissions procedures in federal court. In March 1996, the court ruled in her favor, presumably ending race-based
admissions at the University and the region covered by the fifth circuit.
The class entering the Law School in the fall of 1997 was the first to enroll under the Hopwood ruling. La Griffe's analysis
showed that UT obeyed the law. I reproduced, with his permission, a table from The Color of Meritocracy. In it Griffe
estimates the number of students, by race, who would have been offered admission by rank ordering on cognitive ability.
According to La Griffe, rank ordering would have resulted in 13 offers to blacks and 36 to Mexican Americans. In fact,
these two groups received 11 and 40 offers, respectively, in good agreement with Griffe's estimates. UT Lawyers obeyed
the law.
I added two columns to Griffe's table showing the number of offers to each group using DCT and optimizing for freshman
GPA. I don't have access to the validity coefficients for the admissions criteria used by the Law School, so I spanned a
range using values of 0.5 and 0.6. Under DCT, blacks would have garnered 1 or 2 offers, Hispanics between 7 and 13,
down from 13 and 36, respectively.
1997 Post-Hopwood University of Texas Law School Admissions Data
|
|
Applied |
Offered
Admission
by UT |
Offers by
Rank Order of
Cognitive Ability |
Offers that
Optimize GPA
by DCT
(r = 0.5) |
Offers that
Optimize GPA
by DCT
(r = 0.6) |
|
| white |
2515 |
907 |
909 |
944 |
938 |
| black |
225 |
11 |
13 |
1 |
2 |
| Mex. American |
306 |
40 |
36 |
7 |
13 |
| "Others" * |
(372) |
134 |
134 |
140 |
139 |
Percent of applicants offered admission
|
| white |
|
36.1 % |
36.1 % |
37.6 % |
37.3 % |
| black |
4.9 % |
5.9 % |
0.31 % |
0.96 % |
| Mex. American |
13.1 % |
11.6 % |
2.3 % |
4.2 % |
| "Others" * |
36.0 % |
36.1 % |
37.6 % |
37.3 % |
* "Others" are treated as whites.
|
Brasse. DCT must not leave this room!
Mentor. One of the problems with DCT is that intuitively it seems unfair. How do you explain to an African American
meritocrat that a lower-scoring candidate got his seat? After all, that was the basis of the Hopwood decision. It will not be
obvious to him that DCT and meritocracy have similar goals. DCT optimizes productivity by shrewdly accounting for luck,
thus reducing the effects of chance. It selects the workforce most likely to have the greatest proportion of capable people,
rewarding talent more than any other hiring scheme. Isn't that what meritocracy is about?
High-validity tests also minimize the effects of luck.
Civil rights minded social
scientists would do well to direct some of their energies toward improving standardized tests. Perhaps, when you return to Sandbag, Marcel, you could put a graduate
student on it.
Brasse. I'm afraid pigeonhole menace keeps my group too busy. I am, however, having some second thoughts about DCT.
My success, such as it is, has been in large measure due to my battle against social injustice. Without inequities I would
be timing rats through a maze. Though DCT, itself, is not unfair, it carries the perception of unfairness. Hell,
that's just as good as the real thing. Maybe better! Prodigy, I think I'll take you up on that offer to promote your ideas.
Only I'll have to do it behind the scenes. As DCT catches on, I will beef up my reputation by publicly attacking the theory
as racist mathematics. It's a win-win.
Mentor. Ahem. Prodigy, can DCT guarantee winning the Estati Wager?
Prodigy. There are no guarantees, Mentor. If the molecules in your wine glass were suddenly and concertedly to move in
one direction, the glass might spontaneously fly off the table spilling barolo onto your Bakhtiari. Just as it is a good bet that
your wine will remain in its glass, it is likewise a good bet that DCT will win the Estati Wager. I could do a calculation to
see which is less likely.
Mentor. I'm afraid that will have to wait for another meeting. You have a plane to catch, Marcel, and I am off to lecture.
Prodigy. Yes, and I must clear the snow from Aunt Patricia's walk. It has been a great honor Professor Brasse. I shall
never forget our meeting.
###
APPENDIX: THEORY OF DIFFERENTIAL CUTOFF
Our goal here is to present, for the use of employers and colleges everywhere, a method for selecting workers or students
from a multiracial or multiethnic applicant pool, such that collectively they will be the most productive of all possible selections. For
a racially and ethnically homogeneous pool, the method we are about to present degenerates to rank-order selection based
on test scores.
Human variability being what it is, not even performance itself can predict future performance perfectly. That aside, the
sorting of candidates will usually rely on much less accurate methods of appraisal. Even if a test correlates weakly with
performance, significant gains in productivity can be effected by applying our methods.
Usually, raw test scores and performance assessments will be in different units. It is convenient, therefore, to use standard
units, and we do so throughout.
Consider a circumstance in which an employer or college has NS vacant slots to fill. Applicants for the positions belong to
M distinct racial/ethnic groups, with Nk candidates from group k. Each applicant takes a "test" whose score is used to rank
him among the candidates.
Let: <sk> be the mean test score of
hired or admitted applicants who belong to group k;
<gk> is the mean job performance of the hires (or GPA of admitted freshmen) from group k; rk
is the kth group validity coefficient, i.e., correlation between test score and performance for that
group; and
Δk
is the test score mean difference (white minus group k) between whites and group k members in their respective at large
populations.
It is convenient to choose an origin for the test score. Accordingly, we set the mean score of the greater white population to
zero. Thus, for whites, Δk = 0. With this choice of origin, the kth population mean becomes -Δk, and (<sk> + Δk) represents
the mean score difference between hires (or freshmen) from group k and the general group k population.
Regression to the mean establishes the relationship between mean test score and mean job performance, i.e., <gk> = <sk> -
(1 - rk)(<sk> + Δk). Or simplifying:
<gk> = rk <sk> - Δk (1 - rk)
(A.1)
A candidate from group k will be hired or admitted if his test score equals or exceeds his group's cutoff score. The cutoff
scores will be chosen to maximize productivity of the hires or freshmen.
Let nk be the number of applicants selected from group k. The total output, G,
of the hired workers or the freshman class is
then

Total output, G, might be measured by the number of widgets
produced per week or the total number of grade points earned by a
freshman class.
Now vary the cutoff scores, λk, so as to maximize G. For small variations in the cutoffs, δλk, there will be a corresponding
variation ΔG, which vanishes at the extremum, i.e.,
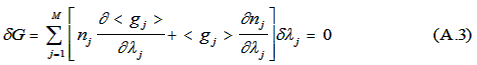
The number of applicants selected is constrained by the number of available slots, NS. That is, the only interesting values
of the λk are those which satisfy:

or, more conveniently, satisfy:

Applying the Lagrange multiplier, α, to (A.5) and subtracting the result from (A.3) gives:
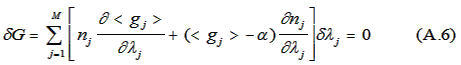
Equation (A.6) is satisfied when the coefficients
of the δλj vanish, giving the M equations:
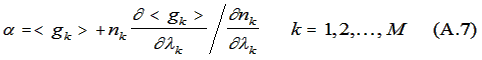
Let Pk(x)dx be the probability that a group k
member has a test score between x and x +
dx. Then the fraction of group k members, fk, whose test scores equal or exceed λk is given by

Also, we may write

Combining (A.1), (A.7), (A.8) and (A.9) yields after simplification:
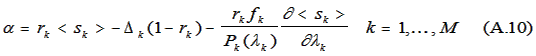
Noting that
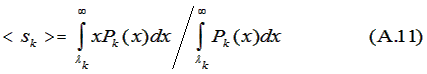
the derivative in (A.10) may be evaluated and (A.10)
further simplified to yield:
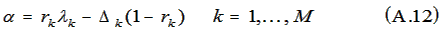
The M equations, (A.12), plus the condition
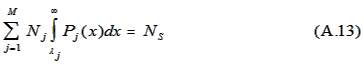
uniquely determine α and the M cutoff scores, λk, that maximize
productivity.
The kth term on the left side of (A.13) represents the number of people hired from group k. Equation (A.13) simply requires
that the terms sum to the number of available slots.
# # #
|