HOW AN IQ TEST CHANGED THE COURSE OF HISTORY
 

   I walked the four steps up to Mentor's door and knocked. I had called to thank him for his counsel and forbearance throughout the year nearly gone, and to wish him well for the year to come. He showed me to his study. From its appearance I gathered that Mentor was engaged in an undertaking that left no time for straightening up. The grey circles under his eyes told me he had been working all night. On the table, next to his computer, lay stacks of printout, amidst them an empty bottle of barolo.

   "You are busy," I said, "perhaps I should return another time." 

   "No, no Prodigy, please stay. I have been occupied with a trivial matter, though it has beguiling aspects."

   I had in my twelve years become familiar with Mentor's addiction to understatement, and could see that he was more pleased with himself than his words implied. He reached into a drawer and withdrew a packet of newspaper clippings. Fingering through them, he removed a creased page and thrust it into my hand. "Read this," he directed.

   It was a Charles Krauthammer article from the Washington Post of December 15. Circled in pencil was a single line, which I read aloud:

" 'We'll never know who "really" won (because the margin of victory is smaller than the margin of a vote-counting error).' 

   "I am afraid Krauthammer was wrong," said he. "Not only do we know who won, we know the margin of victory."

   I waited for Mentor to continue, but instead he took back the Krauthammer piece and sat silently staring at it. Seconds passed before he looked up and resumed: "In your reading of the newspapers following the election, did you not find it odd that time and again the notion was advanced that poor people, mostly black, were forced to use cheap punch-card systems, causing high error rates in traditionally Democratic constituencies?"

   "It is common," I suggested, "for people to interpret facts according to their weltanschauung."

   "Exactly, Prodigy. Thus, when Rev. Jackson cried: 'Blacks were disenfranchised,' the press was all too eager to provide a sounding board for his theme. Here, for example, in the New York Times of December 26 we find:

" 'A higher percentage of black voters were required to use the cheaper, less efficient punch-card systems to register their choices, while whites tended to vote in more affluent districts with more reliable optical scanning systems.'

   Mentor retrieved a page from The Washington Post of December 27. He read aloud:

" 'Poor people are more likely to invalidate ballots because of their unfamiliarity with punch-card systems,' said [Herb] Asher, [the Ohio State University voting specialist] citing a study of his from 1978, when Ohio first used the equipment. Voters in well-to-do suburbs disqualified their ballots 2 percent of the time, he said, while voters in poor black areas did so as much as 20 percent of the time.'

   Mentor fished out a Washington Post clipping of December 3, "Here, the point is made by Post staffers, John Mintz and Dan Keating:

" 'Heavily Democratic and black neighborhoods in Florida lost many more presidential votes than other areas because of outmoded voting machines and rampant confusion about ballots, according to a precinct-by-precinct analysis by the Washington Post. 

" 'As many as one in three ballots in black sections of Jacksonville, for example, did not count in the presidential contest. That was four times as often as in white precincts elsewhere in mostly Republican Duval County.'

   Mentor caught me by surprise. I had listened with the greatest interest, but could find nothing compelling in the news clips. "I see nothing remarkable," said I.

   Mentor rose from his chair and walked to the window. With his back to me, he spoke in a slightly elevated tone that communicated his annoyance: "On the contrary, Prodigy, you see everything. You fail, however, to reason from what you see."

   "How about a hint?" I asked.

   "Look at the numbers, Prodigy. What do they tell you?"

   "Well," said I, "we have two instances in which ballots cast by blacks were found to be deficient at a higher rate than those of whites. In one case 20 percent of black ballots were tossed out for voter error, compared to 2 percent for whites. In another, 1/3 of the ballots cast by blacks were disqualified compared to 1/12 for whites. Both examples show blacks to be significantly more in error than whites. In the first example, blacks erred at 10 times the rate of whites, in the second, at 4 times the rate. Both examples illustrate a higher error rate for blacks, but they disagree quantitatively."

   "On the contrary, Prodigy, they agree perfectly."

   "I'm afraid I am missing something, Mentor."

   Mentor scratched his head (I fear in disapproval). "Have you read the December issue of La Griffe du Lion," he queried, "the one in which the method of thresholds was developed?"

   "Yes of course, La Griffe showed how it is possible to assess group differences in a trait from the proportions of the groups that reach some threshold. I recall, for example, that he used venereal disease as a threshold to assess group differences in sex drive."

   I had a flash of insight. "Casting a ballot properly is a cognitive challenge," said I, "albeit a low one. In the Griffian sense, it is a cognitive threshold. Thus, from the proportions of blacks and whites who meet this challenge, the method of thresholds can give us the black-white cognitive gap."

   I leaned back in my chair, but my self-satisfaction was not to last.

   "The black-white cognitive gap is well known," shot back Mentor. "I am not in the business of rediscovering old knowledge, and certainly the crude one-digit data from the Post will not improve our estimate of the black-white cognitive gap. Though these data do not contribute to our understanding of the gap, they do suggest how to interpret the Florida election results."

   "How so, Mentor?"

   "Apply the method of thresholds to the data in the news clippings. Use my computer; I have coded an algorithm for the method."

   It took but a moment to do the calculation. "The two examples yield black-white cognitive gaps of 1.2 and 0.95 standard deviations (SD), respectively," I announced. "With one-digit input, however, we get one-digit output. Thus, to the accuracy of the data, both examples yield the same 1 standard deviation black-white cognitive gap."

   The data snippets from the Washington Post, though at first appearing to be quantitatively contradictory, were in fact congruent, affirming the proposition that voting is a cognitive hurdle, and also that the relative black and white error rates were consistent with established psychometric measurements of IQ. "Is that the key to decoding the Florida election results?" I asked.

   "Precisely, Prodigy."

   I was a bit depressed. With the facts before me, I had neither recognized their importance, nor their connection to each other. Mentor sensed the change in my affect. He rose from his chair, pulling it up beside me at the computer. "Prodigy," he said, "we can, from published election results, ascertain just how much of a cognitive challenge each voting system posed to the voters. Come, we will evaluate the minimum IQ needed to successfully vote in every Florida county on November 7, 2000."

   Mentor took a sheet from atop of a stack of printout. Turning it blank side up, he proceeded to make a sketch.

   He elaborated: "I have drawn, for some fictitious county, the IQ distributions of black and white voters. The distributions are displaced from one another by 1 standard deviation. The minimum IQ needed to use the voting apparatus is labeled as the 'ballot casting threshold.' It will vary from county to county because of the assortment of equipment, ballot designs, and software used throughout Florida.

   "Voters with IQs below the threshold will be unable to vote correctly, and their ballots will not be counted. The number of such uncounted ballots equals the sum of the areas under the curves to the left of the threshold. To determine the IQ threshold, we merely shift it to the point where this sum of areas equals the published number of uncounted ballots. It is that simple, Prodigy.

   "Once the threshold is obtained, the area under each individual curve gives us the number of uncounted ballots cast by each race. Thus, though such information is neither published nor directly known, we are able to partition uncounted ballots into those cast by whites and those cast by blacks."

   "Mentor," I asked, "would you mind if I write this up in my journal?"

   "I would be honored," he replied.

   Mentor retrieved a crumpled slip of paper from the waste basket. He smoothed it on the tabletop. "Here is the algorithm needed to do the computations. You may include it in your account."

   It had been written in great haste, but was altogether legible. I folded it neatly into  my shirt pocket for inclusion herewith as an appendix.

   "To perform the calculation you require the numbers of voters of each race," I commented. "How did you obtain them?"

   "I used the 95.6 percent solution."

   "And what, sir, is that?"

   "But for the unwitting cooperation of the Democratic Party and the NAACP, I would have had difficulty partitioning the voters into blacks and whites. Their operatives, however, working with great industry, and with a substantial budget, turned out blacks in unprecedented numbers. On election day they even ferried black voters to the polls. Overall, 893,000 blacks voted, an astounding 95.6 percent of the 934,261 black registrants. Such near-total participation could not withstand much local fluctuation and maintain itself. Thus, I assumed the 95.6 percent turnout to apply individually to each county. The number of registrants by race was supplied by the Florida Department of State, and I determined the number of white voters by difference, assuming a black and white universe.

   "Here is a summary of my key findings," said Mentor as he retrieved a table to the screen.

   Mentor printed a copy for my journal (reproduced below). "At least 12 different voting systems were used in the Florida 2000 general election," he said, pointing to the first column. "Their names are annoyingly long, so I have coded them 'A' through 'L' in the table. I will provide you with a key to the names for your journal.

   "Each voting system presented a different cognitive challenge to the voters. Column 2 lists the minimum IQ required to use each system properly. Because voter IQ is probably higher than that of non-voters, but by an unknown amount, I expressed IQ as a number of standard deviations from the white-voter mean, rather than conventional IQ units. Consequently, should you wish to convert to conventional IQ units by taking one SD as 15 IQ points, add a few points -- perhaps two or three -- to your result.

   "The best voting system was 'L,' an optical scanning system from Global Election Systems, Inc. Adopted by 17 counties, it required only an IQ of about 60 to use correctly. Before PC, people with IQs of 60 were classified as morons. 'Mildly retarded' is now more acceptable. They are capable of acquiring reading and arithmetic skills to about sixth-grade level.

   "The most difficult system was 'A,' from Sequoia Pacific System, Corporation. This punch-card system, adopted by 2 counties, required an IQ of about 75 to use. Though not qualifying for rocket science, 75 is enough to disqualify more than 25 percent of blacks and 5 percent of whites. Compare this to the Global Elections system which would stump only 3 percent of blacks and a negligible fraction of whites."

   "Can you tell what the Florida outcome would have been if idiot-proof voting systems were used?" I asked.

   "Indeed we can," said Mentor, retrieving another table to the screen.

   "Look here," he said, "using cumulative data for all Florida, I computed the statewide IQ threshold to be -2.19 SD, and from this, calculated overall black and white error rates. Applying these to the turnouts, I found the number of uncounted ballots cast by each group.
 

   "An 11.7 percent error rate for blacks caused 105,000 presidential votes to go uncounted. The white error rate of 1.4 percent resulted in a loss of 75,000 ballots.

   "From exit polls we know that 57 percent of whites supported Bush, with 40 percent backing Gore. Only 7 percent of blacks supported Bush, 93 percent going for Gore. Applying these percentages to the uncounted ballots, we find that Gore lost 127,000 votes to voter error. Bush lost 50,000. Had there been no voter error, with all voters recording their true intent, Gore would have picked up a net of 77,000 votes, enough to defeat Bush handily in Florida, and award him the presidency."

   With that, Mentor had reached his bottom line. His mind was already elsewhere. He gave me a few additional tables to include in my journal. They are appended, unedited, to this account.

   I thanked Mentor for his patience, and extended my best wishes for the New Year. Walking home in the bitter cold, I reflected upon my visit.

Mentor's Algorithm

   Let N_W and N_B be the number of white and black voters, respectively, who use a particular voting system. Let P(x) be the normalized IQ distribution of the white voters. If the black-voter IQ distribution lags behind the white by Δ > 0, but is otherwise similar, then the normalized IQ distribution of the blacks is P(x + Δ).

   Let x₀ be the minimum IQ needed to use the voting system correctly. Then,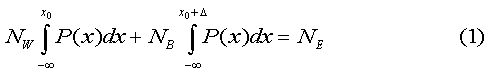

where N_E is the total number of ballots cast in error, i.e., the number of voters who fail to meet the cognitive requirements for voting correctly.

   In (1) we have used the transformation:

   Knowing the cognitive gap, Δ, (taken here to be 1 SD), we may numerically solve (1) to obtain the minimum IQ needed for voting properly, i.e., x₀.

   The numbers of uncounted ballots cast by whites and blacks, respectively, due to voter error, may then be obtained from the expressions:

and

Additional Tables: