A crisis of violence   
   John is white. He is married with two children. He wears a blue collar when he leaves his shabby, inner-city house to go to work. Life has been a struggle for John, but now he faces his most difficult challenge. John's neighborhood is turning black.  

   In John's city, neighborhoods do not integrate, they go black. He has seen it happen elsewhere. He knows what to expect. John and his family will soon face intolerable hardships. They will have to move. Inevitably the last whites able to leave, will. High among their reasons will be fear -- fear of becoming victims of violent crime. As his neighborhood turns black, John and his family will notice many changes, but none will be more dreaded than the prospect of being violently victimized.  

   We will model violent crime in John's neighborhood, tracing its evolution as the community goes from all white to all black. We will chart the course of victimization from insidious beginnings to the threshold of intolerability. We will show that initially the swelling danger will be barely noticeable, but from the beginning there will be an underlying acceleration that ultimately will drive the risk to extreme levels.  
  

The data  
   The data reveal two causes of white victimization by blacks. First, a black is 3 times more likely than a white to commit violent crime. However, as a neighborhood turns black, this factor could increase black-on-white violence at most by a factor of 3, and then only when a neighborhood is virtually all black. The observed level of white victimization is much too high to blame on general tendencies of blacks to be violent. A more important reason is simply that blacks prefer white victims.  

   The best and most complete evidence comes from the Justice Department. Its annual National Crime Victimization Survey (NCVS) canvasses a representative sample of about 80,000 Americans, from roughly 43,000 households. From this survey, a picture of crime is painted by its victims. The last full report of the NCVS was issued in 1994. From it we learn that blacks committed 1,600,951 violent crimes against whites. In the same year, whites committed 165,345 such offenses against blacks. Despite being only 13 percent of the population, blacks committed more than 90 percent of the violent interracial crime. Less than 15 percent of these had robbery as a motive. The rest were assaults and rapes.  

   The asymmetry of interracial crime goes still deeper. More than half the violence committed by blacks is directed against whites, 57 percent in 1994. Less than 3 percent of the violence committed by whites is directed against blacks. Population and NCVS statistics reveal that in 1994 a black was 64 times more likely to attack a white than vice versa. In the city, the races live mostly apart from one another, so that the most convenient victims of thugs are others of the same race. Only a hunter's mentality could account for the data. Given a choice, a black thug will select a white victim. Ironically, so will a white thug.  
  

Modeling the Hood   
   The real world is too complicated for us to describe exactly. We can learn about it by describing a simpler system, or model, that mimics it. The model should include the essential features of the real system, and yet be mathematically accessible. Refinements can bring us closer to the truth, but we never quite reach it. We approach truth asymptotically. To model John’s neighborhood, we face a problem immediately. A neighborhood is itself an abstraction. Where does it begin? Where does it end? We simply regard John's neighborhood as a black and white universe with a total population N, a black fraction f_B, and a white fraction f_W.  

   Divide the number of criminally violent victimizations perpetrated by blacks in a year, by the black population and call this quantity, p_B. It is related, but not equal, to the probability that a randomly selected black is a violent criminal. It would be that probability if criminals always acted alone and committed only one violent act per year. Since we are interested in victimization, p_B is the more relevant quantity. The corresponding quantity for whites is p_W.  

   The probabilities calculated below refer to a one-year period. First we look at the probability, Φ_B, that a particular white, say John, will be victimized at least once by blacks. The white population in the hood is Nf_W. Consistent with NCVS data, we assume that if presented with a convenient choice, both black and white thugs will select white victims over black. Then, the number of incidents involving white victims and black perpetrators is p_Bf_BN. For simplicity, we assume single-victim incidents. (This does not preclude victims from being attacked more than once a year.) The probability that John will be the victim in Incident 1 is 1/(Nf_W). The probability that John will not be that victim is 1-1/(Nf_W). The probability that John will not be the victim of Incident 2 is also 1-1/(Nf_W). If each incident is independent of the others, the probability that John will not be victimized by blacks this year is (1-1/(Nf_W))^(p_Bf_BN). The probability that John will be victimized within the year is then  
  

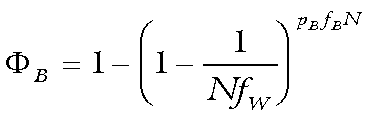                  (1)

   The probability, Φ_B, may be conveniently approximated when Nf_W >> 1, a condition met in every practical circumstance. The approximation will be seen to hold over the useful range of the function. It may be obtained by noting that the second term on the right hand side of (1) is of the form (1 - ε)^n, where ε << 1. If y = (1 - ε)^n, we may write ln y = nln(1 - ε). For small ε, ln(1 - ε) ≅ -ε (the linear term in the expansion about ε = 0), so that ln y ≅ -nε. Exponentiation gives back the approximation, (1 - ε)^n ≅ exp(-nε). Accordingly, we write for Φ_B  
  

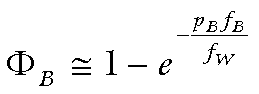                               (2)

   The approximation (2) is attractive because it has no explicit N dependence. To a high degree of approximation, the size of John's neighborhood will not change the likelihood of him becoming a victim. For N = 1000 and p_B = 0.0858 (estimated from the NCVS below), we computed Φ_B from (1) for various black neighborhood fractions, f_B. For the same value of p_B, we also applied the approximation (2). The results are compared in the table below. Agreement is excellent throughout the range of racial composition.  
  

Results  
   Figure 1 traces the evolution of black-on-white violent crime as a neighborhood transforms racially. The probability, Φ_B, that John is victimized at least once in a year is plotted versus the black fraction of the neighborhood. Beginning insidiously, the preying of black upon white is barely noticeable until the community is about 20 percent black. At that point, the probability of John being attacked by a black is still only 0.02. However, the probability that at least one member of John's family will be attacked by a black is about 8 percent. When the black population grows to 50 percent, the likelihood that John will be attacked by a black rises to 8 percent, and the chances are 29 percent that someone in John's family will be attacked within the year. For most whites, this threat crosses the threshold of intolerability, but those more hardy or less able will remain. As blacks begin to predominate, the situation for whites grows worse rapidly. If John hangs on until his neighborhood is 65 percent black, the risk of victimization will be 15 percent for him and 53 percent for his family. Should John be among the most foolhardy hangers on, when the black population reaches 90 percent, John will have a 54 percent chance of being victimized by blacks, with the chances of someone in his family becoming a victim being better than 95 percent -- a virtual certainty.  

Risk from whites  
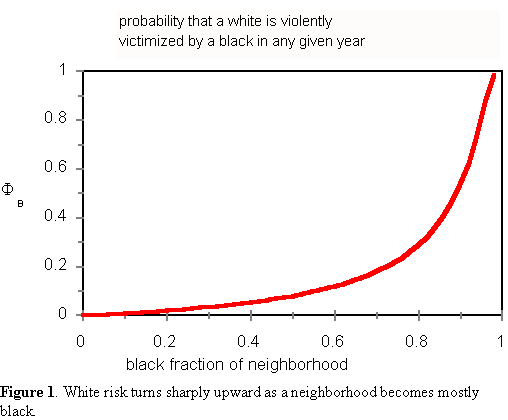   Our model paints a bleak picture for John, but since he grew up in a tough blue-collar neighborhood, he is not new to risk. Let us see how his new post-integration risk compares with his pre-black risk. To do this, we calculate the probability, Φ_W, that John will be victimized by whites.  

   Regardless of the state of racial mixing, the number of victimizations per year perpetrated by whites in the hood is given by p_Wf_WN. The probability that John will be the victim of white-on-white Incident 1 is 1/(Nf_W). The probability that John is not that victim is 1-1/(Nf_W). The probability that John is not the victim of Incident 2 is also 1-1/(Nf_W). Again, assuming independent incidents, the probability that John is not victimized by a white in the given year is (1-1/(Nf_W))^(p_Wf_WN), and the probability, Φ_W, that John is victimized by whites is  
  

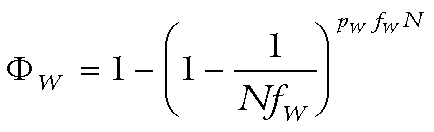           (3)

   The probability, Φ_W, may be approximated by similar methods used to approximate Φ_B, giving Φ_W ≅ 1 - exp(-p_W). We can make a further simplification here. Since p_W << 1, we may write exp(-p_W) ≅ 1 - p_W, giving us the extraordinarily simple expression:  

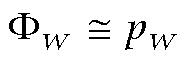                                      (4)

   Equation (4) gives the probability that John will be victimized by a white in a given year. It shows that to a high degree of approximation, the risk John faces from whites is not only independent of neighborhood size, but also neighborhood composition. The probability that John is attacked by whites in a given year is the same no matter where he lives. It is simply equal to the per capita number of violent incidents perpetrated by whites in a year. We tested this approximation, setting N = 1000 and p_W = 0.0279, the value obtained from the NCVS. Over most of the range of racial composition, the approximation, Φ_W = p_W = 0.0279 agrees within 2 figures with the accurate expression (3) as seen in the table below.  
  

Total risk   
   Finally, we want to compute John's total risk of victimization, that is, the risk of being attacked by anyone, white or black in a given year. The probability of John not being victimized by a black is 1 - Φ_B, and for not being victimized by a white, 1 - Φ_W. The probability that he is not victimized at all is (1 - Φ_B)(1 - Φ_W). Therefore, the total probability, Φ, of John being victimized in a given year is 1 - (1 - Φ_B)(1 - Φ_W), or  
  

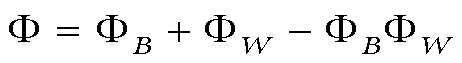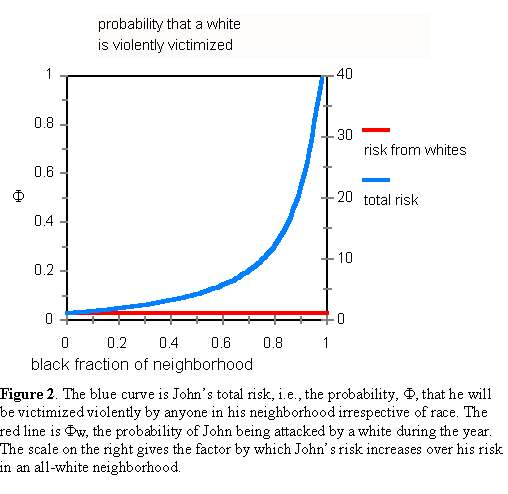
          (5)

   In Figure 2, we plot the probability, (in blue) that John is violently victimized by anyone from his neighborhood, irrespective of race during the year. Also shown (in red) is John's risk from white thugs. Because John knew crime before his neighborhood began to turn black, we are also interested in comparing his post-integration risk with his pre-integration risk. The scale on the right side of Figure 2 shows the factor, Φ/Φ_W, by which John's risk has increased since blacks moved into his neighborhood.  

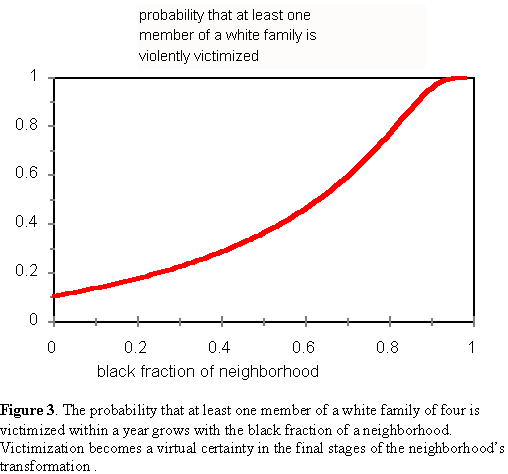
   The probability that at least one member of John's family will be violently victimized in any one year is simply 1-(1-Φ)⁴. Figure 3 shows how this probability varies with the neighborhood's racial composition. In a 50 percent black neighborhood, there is a 37 chance that John's family will in some way be violently victimized. As the neighborhood relentlessly turns black, some whites will have to be among the last to leave. If John is unfortunate enough to be one them, he will face the following statistics: When the neighborhood is 90 percent black, John and his family will have a 96 percent chance of being victimized. Soon after that victimization will become a virtual certainty, reaching 99 percent likely when the neighborhood turns 93 percent black.  

Summary  
   We have modeled violent victimization of whites in a racially mixed neighborhood. Our model is based on data collected by the Justice Department and reported in the NCVS. It paints a bleak picture for whites. As a neighborhood turns black, violent victimization of its white residents begins immediately. At first the risk is small, not much different from its previous all-white level. However, by the time the neighborhood reaches the half-black point, every white family of four has better than a one in three chance of being victimized within a year. Two factors account for black-on-white violence. 1) Blacks are 3 times more likely to commit violent crime than whites, and 2) black thugs prefer white victims, selecting them 64 times more than white thugs choose black victims. Most of the risk faced by whites, results from the predilection of black thugs to prey upon whites. As a neighborhood becomes overwhelmingly black, the risk curve for whites rises to ominous heights. In the last stages of transformation, the likelihood of a white being victimized within a year becomes a virtual certainty.