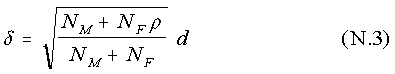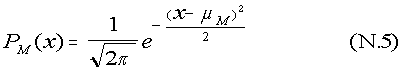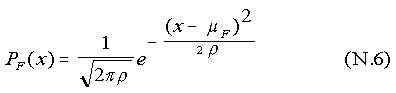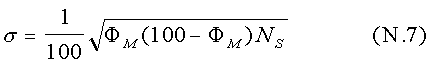|
||||
HOME contents of La Griffe du Lion Write La Griffe |
Prodigy's Journal, July 2005 President of Harvard, Lawrence Summers, speaking informally in January at the National Bureau of Economic Research Conference on Diversifying the Science & Engineering Workforce, observed:
It had been three weeks to a month after Summers' ill-advised remarks that I came to think about them in a quantitative way. And just now do I write about them. President Summers had momentarily dropped his guard. It was, after all, a meeting of confreres closed to the public and the press. In the ensuing weeks, Summers offered an abject apology, received a vote of no confidence from his Faculty, and Harvard coughed up $50 million to promote gender equity. For such a handsome sum President Summers might have provided the Conference with some extra detail, perhaps along these lines . . . Summers Redux My first priority as President is to preserve and encourage high standards of scholarship. The Cornell West affair attests to my sincerity in this regard. However, I am also committed to promoting campus diversity. Regrettably, the two goals are often at odds -- a problem that faculty woefully underappreciate. The Department of Mathematics will illustrate. Like most departments at Harvard, its quality is exemplary. Approximately 40% of its full professors (including emeriti) have been elected to the National Academy of Sciences, as you know a high distinction. Of its approximately 2000 members (I see several here today) more than 190 are Nobel Laureates. A dozen universities account for roughly 45% of the membership. Like peas in the same high-end pod, they face common difficulties diversifying faculty. Table 1 lists them in rank order as they stood in 2003. There is some juggling of position from year to year, but the universities at the top of the list are always immediately recognizable as major research institutions.
The Fields Medal is arguably the highest honor accorded a mathematician. Three Department members (including emeriti) are Fields Medalists. The Medals, established in the will of John Fields, were first awarded in 1936. Suspended during WWII, the awards resumed in 1950 and have been conferred quadrennially since. To date there have been 44 Medalists. But I come not to brag about our Mathematics Department. I have, after all, had nothing to do with its eminence. Rather, I mean to use the Department to demonstrate the difficulty of bringing senior female faculty onboard, while at the same time maintaining its quality. Many in this audience have been harshly reproachful of the scant representation of women among the ranks of full professors, especially in math-intensive fields. But before you take me or the University to task we need to ask what outcome we can reasonably expect when talented researchers compete for these positions. More precisely, if the slots are filled in rank order of ability, what percentage of them will be occupied by women? To answer, we need to know how mathematical ability is distributed by sex. The scientific literature abounds with studies of cognitive sex differences. From them we learn that cognitive gender gaps appear early in life, that girls display greater verbal ability, boys greater mathematical ability, that the mathematics gap increases gradually with age until the onset of puberty, when a rapid increase brings it to full flower by mid-adolescence. And that two features characterize the gap -- a higher male mean and a greater male variance. A large majority of the studies describing cognitive sex differences are flawed. The list of issues is long. Samples are often too small to yield significant results. Variances are mostly ignored. Tests with minimal g-loading, like those of the NAEP, mostly measure attainment rather than reasoning ability. Other tests, like the SAT and ACT are taken by nonrepresentative segments of the population. Studies of pre-adolescents are not useful to us because cognitive sex differences have not yet fully developed. Finally, meta-analyses incorporate all the flaws of their component studies, and usually weight them by sample size rather than quality. Among the studies avoiding these pitfalls is the Project Talent1 study of 1960. It remains one of the best assessments of cognitive sex differences in a complete age group ever made. The sample was designed to be representative of all 15 year-olds in the US. It included more than 73,000 15 year-olds, both students and nonstudents. They were given an all-day battery of 23 cognitive tests. The mathematics results revealed a mean (male-female) difference of 0.12 standard deviations2 and a 1.20 (male/female) variance ratio. The corresponding distributions are shown in Figure 1. 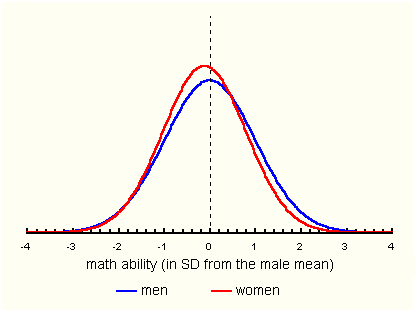
I would like everyone here to now consider the following problem. Its solution will tell us more about gender inequity than an infinity of National Bureau of Economic Research conferences.
The solution is obtained simply by requiring that at the end of the selection process the number of slot holders equals the
number of slots. That is,
We introduce a simplification, made possible when equal numbers of men and women form the pool of competitors, a condition approximately satisfied in all our examples. Setting NM = NW = N /2 in (1) gives: 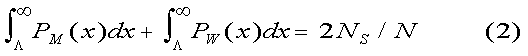
The gender makeup in the winners' circle is conveniently expressed as the male percentage of slot holders,
ΦM , which
using (2) to eliminate
Figure 2 shows how the percentage of males among slot holders varies with the competitor to slot ratio. The curve was calculated from (3), using Gaussians with variances and mean differences from Project Talent. Note how the proportion of men increases as the competition grows stiffer. At 100 competitors per slot, more than 70 percent of slot holders are male. At 1000 competitors per slot, men fill 80 percent of the slots. 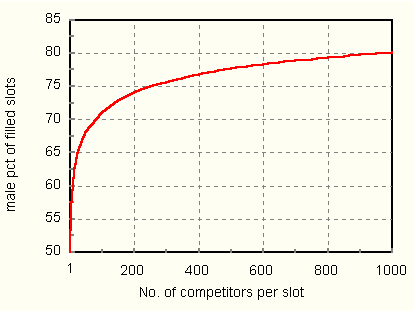
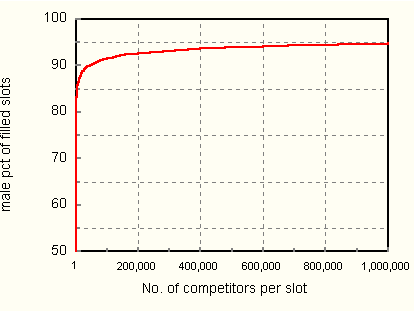
Figure 3 illustrates how the male percentage among slot holders varies in a supercompetitive environment, with up to a million competitors per slot. As the competition becomes more demanding, the male percentage among slot holders increases rapidly before slowing to a crawl.
The pool of competitors is roughly the number of Americans between the ages of 25 and 85, approximately 190,000,000. Setting N = 190,000,000 (the precise value is not important3) and the number of slots NS = 143, the competitor to slot ratio, N /NS , is 1.329 million. With this value in (3), we find that the most probable number of women in the group of 143 Academy mathematicians is 7.1. (I choose not to round to the nearest integer.) At this time there are precisely 7 women in the mathematics sections of the Academy. (The agreement is almost embarrassing.) The 95% confidence interval4 is [2,12]. The minimum mathematical ability among the 143 Academy members is 4.68 SD greater than the male population mean. This is indeed an elite bunch! Sex differences in both mean and variance contribute to the preponderance of men in the Academy, but they contribute
unequally. At this level of ability men predominate mostly because of their greater variability. If we set the mean difference
to zero and redo the calculation, men would constitute 91% of the Academy
membership, down from 95%, but still a hefty majority. Alternatively, if we set the variance ratio to unity,
leaving the means intact, the male representation drops substantially to 64%. Fields Medalists The Putnam Competition The exam itself is punishing -- twelve questions worth ten points each for a total of 120 points. It has been called the world's hardest test. In spite of the blue-ribbon nature of the competition, the median score is typically one or zero. Over the years many top Putnam finishers have gone on to become distinguished mathematicians. Three (John Milnor, David Mumford and Daniel Quillen) are Fields Medalists and two (Richard Feynman and Kenneth Wilson) won the Nobel Prize in Physics. Applying our methods to the Putnam Competition, we first estimate the most probable number of women among the top 200 finishers. The pool of potential competitors, N, includes everyone of college age, not just college students. A four-year span in the neighborhood of ages 18 to 21 includes about 5.5 percent of the population or about 17 million. Crunching the numbers with N set to 17,000,000 and NS to 200, we estimate the most probable number of women to finish in the top 200 to be 17.3, with a 95% confidence interval [10,25]. Last year (2004), 19 women finished in the top 200, in good agreement with our estimate. The minimum ability among the 200 is 4.1 SD greater than the male population mean. The top five Putnam finishers are published in alphabetical order. We don't know how they rank within this group. The five are known as Putnam Fellows. Setting NS = 5, we find that the probability of a random Putnam Fellow being female is 0.041, and that the minimum ability of a Putnam Fellow is 4.9 SD greater than the male population mean -- a bit higher than that of National Academy members. From 1995 to 2004, there have been 38 different Fellows (some competitors win more than once). Three of the 38 were women. Assuming 38 Fellows per decade typical, the probability of at least 3 female Fellows in any given decade is 0.20. Since women have not competed seriously for most of the years the Putnam Competition has been held (the first year was 1938) it remains to be seen whether the most recent decade was one of the five for which we predict at least 3 women Fellows to emerge. The previous decade saw none.
Related cognitive sex differences may be found in other species, often with similar origins. In polygynous vole species, for
example, males cover wider territories than their monogamous cousins. As a result, they have evolved sex-differentiated
navigational skills very much like humans. Polygynous males navigate mazes faster than females of the same species,
whereas monogamous vole species exhibit no such sex difference.5
From this I conclude that philandering males are
the cause of stereotype threat. Thank you. Q & A Q: Girls frequently get better math grades than boys, even though boys score higher on tests of mathematical aptitude. How do you explain this? And isn't classroom performance linked more strongly to future job performance than test scores? LS: When you say "better grades" I think you mean "better average grades." In a high school math class, we expect to find a narrow male majority of 52% in the top half of ability (obtained by setting N /NS = 2 in (3)). Thus with almost equal numbers of boys and girls on each side of the ability median, a bit of extra industry on the part of the ladies, or more likely a bit of slacking off by the boys could easily tilt the average grade toward the girls. None of this, however, is relevant to job performance in fields like engineering, math or physical science. There, considerably more than average ability is required. The technological workforce will emerge from the more selective fractions of the class, where boys predominate to an extent that is not compensable by extra diligence. The 95th percentile of mathematical ability, for example, will be about 64% male, the 99th percentile, 71% male. Q: If, as you claim, 71% of the 99th percentile is male, that still leaves 29% who are female. What have you done to bring senior female faculty up to this level in Mathematics, Engineering and Physical Sciences? LS: Full professors in Mathematics at Harvard represent ability in the top 0.0001% of the population, not the top 1%. We could therefore reasonably expect to find no more than one or two women at that rank, with two being extremely unlikely. I haven't done an analysis of Engineering and Physical Sciences, but I suspect prospects for women there are similar but less stark. Q: OK, so we can't expect gender equity in Mathematics, Engineering and Physical Sciences at Harvard, but can we at least expect 29% of the workforce in these fields to be women? LS: Not likely. Men and women exhibit other behavioral differences which are apparent almost from birth. To some extent they mirror sex-differentiated behavior in animals. Boys are more aggressive, girls more nurturing. Female babies react more to facial expressions, males to moving objects. By adolescence these behaviors have morphed into girls' interest in social relationships, and boys' interest in machines and devices. Obviously, such divergence of interests influences career choices. Girls lean more toward fields like psychology, while similarly talented men incline toward engineering or physical science. A study6 by Lubinski and Benbow followed the careers of mathematically precocious youth from age 13 to 23. All were in the top 1% of mathematical ability. At age 23 less than 1% of the girls were pursuing doctorates in mathematics, engineering, or physical science, while almost 8% of the boys were. Equal aptitude not withstanding, girls pursued doctorates in biology at more than twice the rate of boys, and in the humanities at almost three times the rate of boys. For all these reasons, we should regard 29% as an upper bound to the percentage of women in the technological work force. In practice, their numbers will be significantly less. Q: If all this is so, why are we meeting here today? A: Good question. We are meeting here today because feminists, in order to support their androgynous fantasies, encourage able young women to enter technological fields even when their interests lie elsewhere. Q: I see several people have left and one has thrown up. Do you think there will be repercussions campuswide? A. Nah. We are, after all, first and foremost scholars, researchers and above all colleagues. Thank you all again.
NOTES 2. Project Talent reports a male-female mean difference of 0.12 SD. The unit "SD" as used in this context means one standard deviation in the ability distribution of the combined male and female population. We prefer a standard deviation unit based on the ability distribution in the male population, because it is invariant to changes in the population mix. Other than the original Project Talent reference to 0.12 SD, all references to "standard deviation" or "SD" should be taken throughout to mean one standard deviation in the male distribution. The remainder of this note provides details of the unit conversion. The casual reader may choose to skip it. In standard units, a mean difference, d, in some property characteristic of two groups, say, men and women, is conventionally computed as:
where the subscripts M and F denote male and female, respectively; the μ's are mean scores, and the σ's are standard deviations (all in test units). The denominator on the right side of (N.1) is the standard deviation (in test units) in the combined population of men and women. It is conventional in the psychometric literature to define the standard unit as the number of test units in one standard deviation of the combined population. Equation (N.1) reflects this convention. We prefer, however, to define the standard unit as the number of test units in one standard deviation of the male population. The advantage of this system is that it is invariant to changes in the population mix. In the new
system, a mean difference, δ,
is computed as:
Combining (N.1) and (N.2) gives the relationship between the mean difference in the new system, δ, and the mean difference in the old system, d.
In (N.3), ρ is the variance ratio (female/male). For the special case where NM = NF , we have
In the new units, σM = 1, and σF = ρ1/2. Choosing the male mean to be zero, the normalized distributions for males and females are written:
3. With N /NS > 106, the gender composition varies very slowly with the competitor to slot ratio (see Figure 3). Consequently, we can tolerate lots of error in the input to this calculation. If, for example, we were to cut N by half to 95 million, our estimate of the most probable number of women would increase from 7.1 to only 8.2. 4. The standard error, σ , was computed as
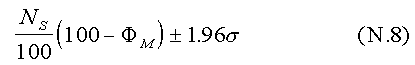
6. Lubinski, D. & Benbow, C. P., Gender differences in abilities and preferences among the gifted: Implications for the math/science pipeline. Current Directions in Psychological Science, 1, 61-66, 1992.
|
||||||||||||||||||||||||||||||||||||||||||||||||
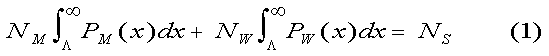
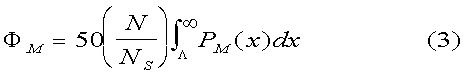
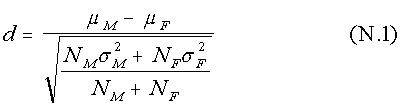
 .
.