 March 2000 |
|
|
 March 2000 |
|
|
STANDARDIZED TESTS:
THE INTERPRETATION OF RACIAL AND ETHNIC GAPS
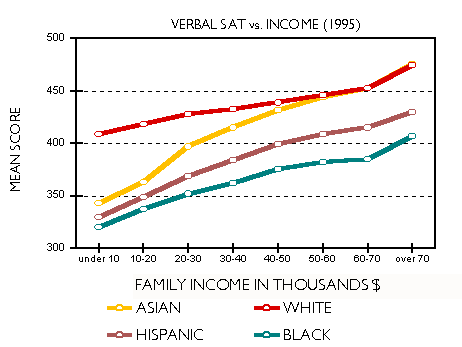
The appearance in our courts of these learned gentlemen of the law, who can make black appear white and white appear black, is forbidden.A Father's Lament Most stories filed each week by wire services end up in the trash. Some make it beyond a circle of regional interest, like the one filed on March 10, 1996 by the Associated Press. It was a story out of Waco, Texas that caught the eye of editors across the country. We read it over breakfast 1500 miles from Waco. It tells of an angry father upset by the failure of his daughter to pass a state high-school exit exam. He decided to do something about it. The story began: WACO, Texas (AP) - When Lester and Coque Gibson's son failed the state's basic skills test eight years ago, they were dismayed. Last year, when their 16-year-old daughter failed, they were appalled. The middle-class black couple had always hoped their children would defy the odds and grasp the American dream. But education is the key. So Gibson demanded an accounting of the school district's test scores. And when he spread the numbers across his desk, he was shocked: Seventy-five percent of the black students and 66 percent of the Hispanic students failed the test in 1995, compared with only 37 percent of the white students. The school district blames poverty and poor parenting for the failure rates. But Gibson blames institutional racism - teachers, he says, have low expectations of minority children. "If we're going to get blamed for the education of our kids, then we may as well take control of their educational destiny and take a shot at it," Gibson said. When kids fail, parents get frustrated. Sometimes they get angry. Lester Gibson got angry. Good test scores mean a lot. Students need them to get into college. Policemen and firemen need them to get promoted. Job seekers need them to get in the door. In Texas you need them to get a high school diploma. All this produces lots of rhetoric, some of it passionate, some of it scholarly, but most of it nonsense. We will try to sort it out. The Waco results are not surprising. We know minorities score lower than whites on standardized exams. However, many scoring scenarios could have resulted. Whites failed at a 37 percent rate, blacks at 75 percent. But what if 50 percent of blacks had failed, or 60 percent or 90 percent? How likely was each of these possible results? We asked this question over breakfast a few years ago. More precisely, we asked: Given a white failure rate of 37 percent, what should we expect for the failure rates of blacks and Hispanics? A few simple assumptions provide the answers. Suppose that the scores of each ethnic and racial group are normally distributed, that is, they fall on or close to a bell curve, like the distribution shown for whites in Figure 1. The distribution is scaled so that the area under it is unity. The white mean in standard deviation units (SD) is zero. The area under the curve from negative infinity to the passing score represents the fraction (0.37) of whites who failed the exam. When the passing score is -0.332 SD, that area is obtained. 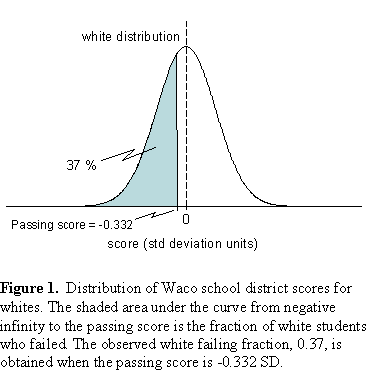 Of all group differences, the best studied is between whites and blacks. The black-white gap is also the most reproducible, the black mean lagging behind the white by about one standard deviation. Consequently, we can estimate the black distribution by shifting the white distribution to the left by 1.0 SD, as in Figure 2. When we do this, the area representing the failing fraction increases to 0.75. That is, if whites fail at the rate of 37 percent, a black-white gap of 1.0 SD implies that blacks will fail at the rate of 75 percent, in agreement with their observed failure rate in Waco. Thus, the Waco school district results for blacks and whites were consistent with standardized test results observed universally. (Details of the calculation are given in Appendix A.) 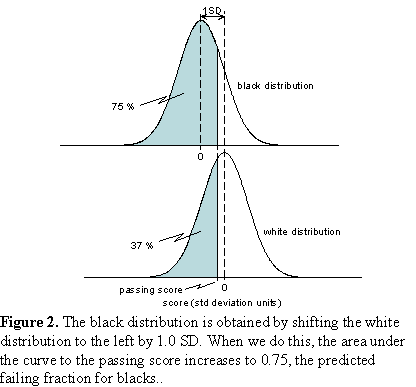 Nationally, the Hispanic-white gap is more variable than the black-white gap. Part of the reason is that the term Hispanic applies to several groups genetically far removed from one another. In Waco most Hispanics are of Mexican descent -- Mestizos. For the Mexican American performance gap we used two sources: SAT scores and data from the 1966 Coleman Report. The College Board divides Hispanics into several subgroups: Puerto Rican, Mexican American and Other Hispanic. The 1998 SAT results yield a white- Mexican American gap of 0.69 SD. The Coleman Report found a gap of 0.84 SD. We used both values to predict a Hispanic failure rate between 64 and 69 percent, bracketing the observed Hispanic failure rate of 66 percent. The Usual Suspects Writing about test scores in the November 1993 issue of The Atlantic Monthly, Duke University professor, Stanley Fish, renowned for scholarship in both law and literature, asserted: "Statistical studies have suggested that test scores reflect income and socioeconomic status. It has been demonstrated again and again that scores vary in relation to cultural background; the test's questions assume a certain uniformity in educational experience and lifestyle and penalize those who, for whatever reason, have had a different experience and lived different kinds of lives. In short, what is being measured by the SAT is not absolutes like native ability and merit but accidents like birth, social position, access to libraries, and the opportunity to take vacations or to take SAT prep courses." Lani Guinier, Professor of Law at Harvard University, writing in the New York Times of June 24, 1997, argues, "But within every racial and ethnic group, test scores go up with family income. One explanation for this may be that students who come from better-off families can afford coaching for the test. Students from wealthier families also have other advantages. They are more likely to have been exposed to books and travel." We know that test scores go up with family income. They also improve with socioeconomic status. Both trends are observed within all ethnic and racial groups. But before you blame income and socioeconomic status for the test score gaps, consider this: Figure 3 shows how math SAT scores increase with family income for both whites and blacks, confirming Professor Guinier. However, black students from families earning more than $70,000 (1995 dollars) score lower than white students whose families earned less than $10,000. Figure 4 shows more of the same for the verbal SAT. Here too, the wealthiest blacks score below the poorest whites. (Complete data can be found in Appendix B.) 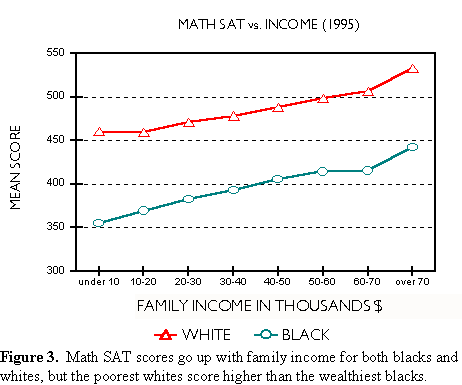 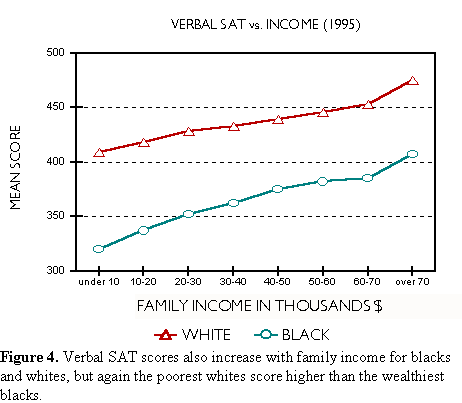 As for "social position, access to libraries, and the opportunity to take vacations or to take SAT prep courses," consider this:
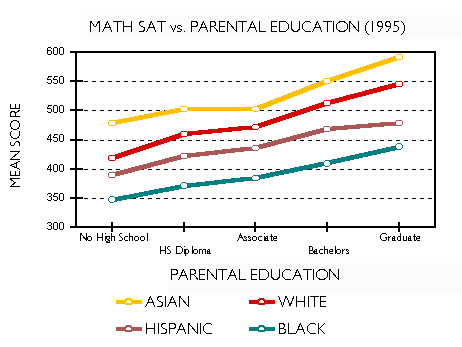
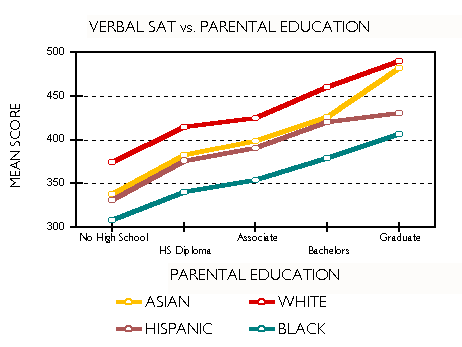
Figures 5 and 6 show, respectively, how math and verbal SAT scores for blacks and whites vary with parental levels of education. In both cases, black children of parents with graduate degrees score lower than white children whose parents have a high-school diploma or less. 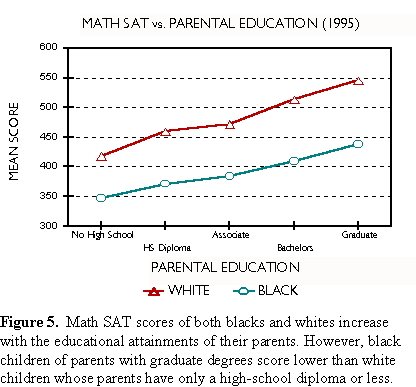
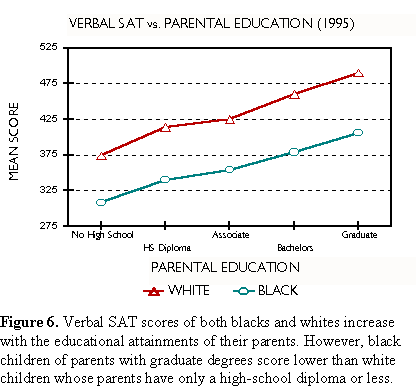 When Professor Fish asserts that test scores reflect income and socioeconomic status, he is, of course, correct. We cannot conclude, however, as he does, that either is to blame for the black-white SAT gap. Figures 5 and 6, show that at every level of income and social advantage the gap exists. In fact, it remains remarkably constant when economic and cultural levels are controlled. Professor Guinier observes that within every racial and ethnic group, test scores go up with family income. Guinier leaves no doubt she is aware in detail of the SAT data. Her syllogism begins, ". . . students who come from better-off families can afford coaching for the test . . . They are more likely to have been exposed to books and travel." We are to complete it with: Minorities have less income and cultural exposure; therefore, minorities have lower scores. More SAT data may be found in Appendix B. There, you will discover that Asians mostly sit on top of the heap; that whites, Mexican Americans and blacks follow in that order. Some details prove interesting. For example, whites enjoy a verbal advantage over Asians that disappears at high levels of income and social advantage. Regrettably, the College Board no longer discloses these data. In 1996, they stopped publishing performance by income and parental education disaggregated by race and ethnicity. Trends in the Gap Test scores sell panty hose. Scores make news. Stories continue to appear months after they are released. Parents fret about them. Politicians demagogue them. Businesses make relocation decisions based on them. Property values vary with school performance, and school administrators put their jobs on the line. Everybody wants high pass rates. Pressure is everywhere. And the racial gap is never far from the surface. Several states have their own statewide exams. Results are usually reported as pass rates, often at several achievement levels. The statewide exams are designed to maintain a constant level of difficulty from year to year, so that changes in performance signal progress or backsliding. A drop of even a few points is cause for hand-wringing. In contrast, improvements are celebrated. Reporters on the education beat and their editors define the racial gap as a difference in pass rates between two groups, one of which is white. This can be dangerously misleading when used to track gap trends. For example, consider the Maryland School Performance Assessment Program (MSPAP). Between 1993 and 1999 the black-white gap for eighth grade math increased from 36.8 to 42.3 percentage points causing extensive hand-wringing. But spare the lotion. The difference between the black and white performance actually decreased slightly over this time. We will explain. Maryland is very candid in reporting the results of its statewide exam. The data are completely disaggregated, making gap analysis possible school by school, county by county, statewide and by race. Table 1 presents eighth-grade MSPAP results for the years 1993 through 1999.
Figure 7 graphically displays the trend in the black-white gap. 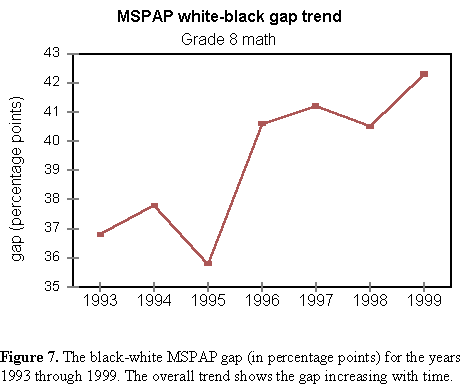 Six years after the 1993 administration of the eighth-grade math test, both whites and blacks show improved pass rates. Whites, however, had improved more. But did they? Pass rate differences are a very arbitrary way to measure racial gaps. Their principal virtue is convenience. If we want to track a difference between two populations, looking at the difference between their means is best. In this way we can see whether the populations are growing together or apart. Given the pass rates of two groups, we can compute their mean difference. (See Appendix A for how.) Table 2 adds the mean difference to the MSPAP data.
Figure 8 shows both computations of the black-white gap displayed graphically. 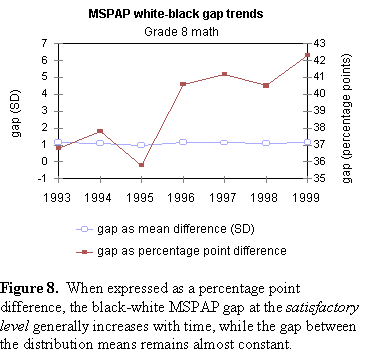
Table 3 shows pass rates at the excellent level, and the corresponding gaps.
Difficulties associated with expressing gaps as pass-rate differences are even more dramatically illustrated in Figure 9. 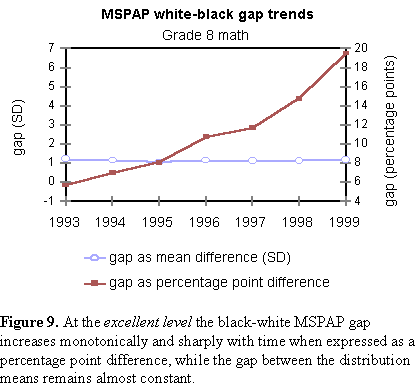
As part of its comprehensive statewide testing program (TAAS), Texas requires its high-school students to pass an exit exam as a graduation requirement. The passing score is 70 percent. Students first attempt the exam in the 10th grade, and if necessary are given seven additional chances to pass. If after eight tries they do not pass, students may continue to take the exam after completing their formal schooling. When ultimately they do pass, they are awarded a diploma. We computed the black-white and Hispanic-white mean differences for first attempts at the exit exam from 1994 to 1999. Figure 10 displays the trends. A small but significant narrowing of the gaps is apparent. 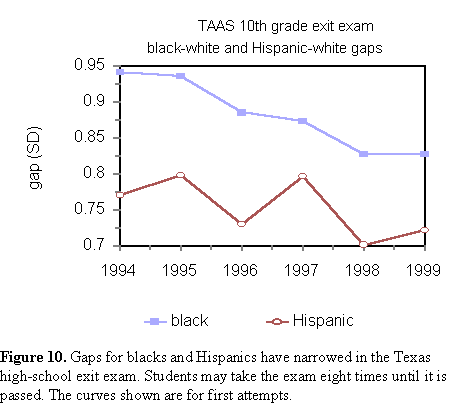 Need a Lawyer? In 1988, New York State's Chief Judge established a committee, The New York State Judicial Commission on Minorities. Its purpose was to study the presence and effects of racism in the state's courts. Buried in its final 2000-page report was the finding that minorities passed the New York bar exam at significantly lower rates than whites. The commission found that for the period spanning 1985 through 1988, first-attempt pass rates were 31.1 percent for blacks and 73.1 percent for whites. Applying the methods of Appendix A, we translated these pass rates to a corresponding black-white mean difference of 1.11 SD. Several years later, commenting on the Commission's findings, Edna Wells Handy wrote in The New York Law Journal of April 1996, "Determining whether those pass rates have remained constant since the Commission's report must await the completion and dissemination of the national bar exam study presently being conducted by the Law School Admission Council." Ms. Handy was referring to the most ambitious study of law students ever attempted. The Law School Admission Council is the organization that administers the Law School Admission Test (LSAT). At the time Handy's article appeared, it was tracking 27,000 students who enrolled in U.S. law schools in the fall of 1991. The students were followed from law school entry to the bar exam. The Council issued its report in 1998, finding that 92 percent of white law-school graduates passed the bar exam on the first attempt, as did 61 percent of black graduates. This implies a black-white mean difference of 1.13 SD. The Council also reported the results of repeated attempts at the bar exam. It found that eventually 97 percent of white and 78 percent of black law graduates passed, corresponding to a black-white mean difference of 1.11 SD. The one-plus SD gap between black and white lawyers stubbornly refused to go away. Others, however, viewed the Council's findings differently. "This study strongly refutes the myth that affirmative action policies tend to set students up for failure on the bar exam," hallucinated Henry Ramsey Jr., a retired California state judge and member of the committee that oversaw the study. Tamar Lewin, covering the Council's report for the New York Times, characterized the Commission's findings as "likely to provide important support for advocates of affirmative action." Her column appeared under the headline: "Minorities Achieve High Success Rate in Bar Exams, Study Says." The fact is that affirmative action has stratified the bar by race and ability. Black lawyers lag behind their white colleagues in measured ability by about 1.1 SD. Affirmative action creates a racial gap at law-school entry that never goes away. When entrance credentials are controlled, racial differences mostly vanish. More than 20,000 adult blacks in the U.S. have an IQ of 130 or more, but because of affirmative action, the chance that your black lawyer will be one of them is vanishingly small. Need a Doctor? Medical school admission is uncommonly competitive, there being many more applicants than slots. The competition is so intense that if black applicants were held to the same admission standards as whites and Asians, we would turn out almost no black physicians. We now have a double standard for admission to medical school brought about by affirmative action. As a result, two tiers of American physicians have emerged separated by race and ability. We have seen that law students admitted under affirmative action do not measure up to their white and Asian peers as law-school graduates. Can we say the same for doctors? We will quantify the performance gap for physicians. A benchmark for medical competence is the National Board of Medical Examiners (NBME) Exam Part I. Every medical student in the US must pass it to become a physician. Students take the exam two years before graduation. It is one of several ways the profession keeps itself honest. The most comprehensive study of NBME pass rates was published in 1994 by Beth Dawson et al (JAMA 1994 272:9 674-9). The authors examined the performance of every medical student in the US taking the June exam for the first time over the years 1986, 1987 and 1988. Dawson and her colleagues found that white medical students passed the NBME test at a rate of 87.7 percent and blacks at 48.9 percent. Again, using methods described in Appendix A, we found these pass rates equivalent to a black-white mean difference of 1.19 SD. Mean differences for the bar and NBME exams are conspicuously similar. The one-plus SD gap does not yield easily. Notably, when Dawson's study looked at entering students with similar academic credentials, the pass rates on the NBME exam were independent of race, pointing an accusing finger directly at affirmative action. For all its good intentions, affirmative action has created two levels of competence in American medicine, separated by a bit more than one standard deviation. When you are wheeled into the ER at 2:00 a.m., if you pray, pray that the black doctor who greets you entered medical school through the front door. APPENDIX A. RELATIONSHIPS BETWEEN PASS RATES AND MEAN DIFFERENCES. Assume all distributions are Gaussian with a common standard deviation. Let P(x) be the probability distribution for whites centered on x = 0. (Standard units are used throughout.) Let Δ be the difference between the white and minority distribution means (white - minority). Then the probability distribution for the minority group is P(x+Δ). If the passing fraction of whites is fW, then the passing score, λ, is given by the solution of:
The distribution function, P(x) is given by
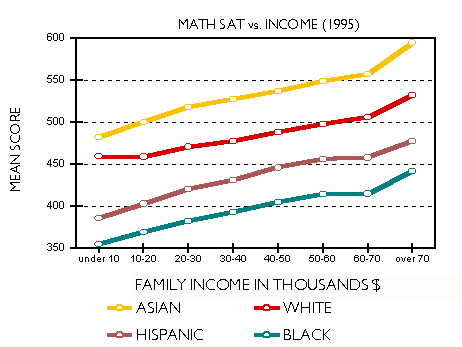
  |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||