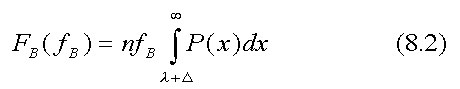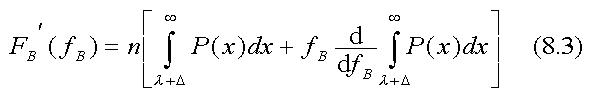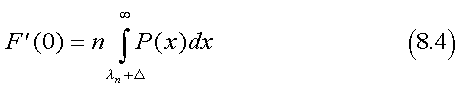 April 2000 |
|
|
|
2048
Mentor. Welcome Prodigy. It's good to see you again. Please come in. Have a cookie and tell me what you've been doing. Prodigy. Thank you, Mentor. I have been toying with the idea of becoming a doomsayer. I believe I could make a living that way and support my researches. Mentor. Something like Einstein in the patent office? Prodigy. Yes, but more lucrative. Mentor. What put you on to this? Prodigy. While visiting Aunt Patricia, I read the 1968 best seller, The Population Bomb. In it, Paul Ehrlich predicted the starvation of 65 million Americans between 1980 and 1989. He subsequently won a $345,000 MacArthur "genius" award, and more recently a $250,000 prize from the Heinz Foundation for his writings on population and nuclear war. With more than a few IQ points on Ehrlich, I should be able to do at least that well. Of course, I would want my predictions to be correct. Mentor. Do you have anything specific in mind? Prodigy. Well yes. In a private communication, Jim Boyd expressed some concern about demographic trends in the US. He pointed out that by mid-century the non-Hispanic white population will have dropped to near 50 percent with Latinos and (to a lesser extent) Asians taking up the slack. Jim suggests, that such a population mix might be destabilizing. High-IQ, high-paying jobs in law, medicine and engineering, for example, would be concentrated among whites and Asians, as now. However, blacks and Latinos with larger combined numbers would have destabilizing political clout. Mentor. Somehow that doesn't seem pessimistic enough to merit a MacArthur or Heinz award. Bill Joy, writing in the April edition of Wired, says that self-replicating technology could wipe out humanity in a few decades. Now that's doomsaying! Prodigy. Let me show you some mid-century population projections anyway.
Mentor. What happened to 2050? Last I looked you had ten fingers. Prodigy. Because Asians, including many Chinese, are projected to make impressive population gains, I thought it prudent to choose a year of the dragon. According to the projection, Latinos will grow to about 24 percent of the population. Combined with blacks, they will be pushing 40 percent. That represents a lot of clout for traditional have-not groups. Mentor. Permit me a brief digression. Look at the points on this graph. 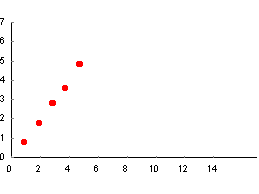 Can you predict where the next point will fall? Prodigy. It might help it you told me what the points represent? Mentor. They represent the charge density, measured by x-ray scattering, along a line through a crystal. Prodigy. Knowing you, Mentor, I smell a rat. The points fall more or less on a line, so you expect me to place a point that extends it, like this. 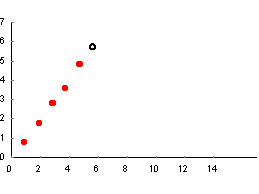 However, the microscopic properties of a crystal are periodic, so without more information I will respectfully decline to place the point. Mentor. Good! Here are the same points, including the new one you declined to add, superimposed upon a plot of the experimental charge density. 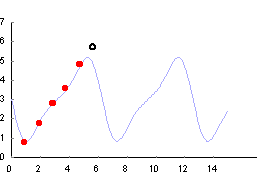 Prodigy. Ha! The rat is exposed. Curiously, the points look squiggly now. Did you move them? Mentor. No, it's an optical illusion that we can explore another time. For now, what can you say about extrapolation? Prodigy. People are eager to extrapolate. I had that impulse just a moment ago, but I exercised restraint. We love to look at small regions in space or time and extrapolate our observations beyond their range of validity. Knowing the local structure about a point in a crystal, we can predict the structure many atoms or molecules away. The crystal's periodicity guides us. Without that model, extrapolation would be a dangerous enterprise. I think it was you, Mentor, who said that extrapolation is a reflection of the ego, and the bigger the ego the bolder the claim. Mentor. Even models may not be enough. Some have so many parameters to plug in, that they become virtually useless. During the Gulf War in 1991, the TV personality and astronomer, Carl Sagan, predicted that burning oil wells in Kuwait would blacken the sky causing the monsoons to fail and bring about mass starvation in southern Asia. He did a worst-case calculation and passed it off as reasonable. Global warming "experts" do much the same thing now. Prodigy. Where do you stand on global warming? Mentor. I remain agnostic. The issue has been so politicized that it is near-impossible to get a balanced picture. My cursory examination of the technical literature indicates that there is plenty of credible dissent. Let's keep that topic open for future discussion. Prodigy. If I go into the futurist business, I promise to be circumspect. Mentor. Well then let's look at your population estimates. Where did they come from? Prodigy. Demographers at the Census Bureau produced them. Their predictions, which extend to 2100, can be found on the Census Bureau website. Mentor. Talk about ego. A change in the world health profile, a small war or two, political realignments, or any of countless unforeseen events could render a hundred year prediction useless. It's a waste of taxpayer money. Prodigy. I should do a calculation to see if such waste can affect my inheritance. Mentor. Perhaps another time. Tell me, what do the demographers see for the total US population at the end of the century? Prodigy. Close to 600 million. Mentor. Do you see that as a problem? Prodigy. Not even close. We can comfortably sustain many times that number. The problem I see has not so much to do with quantity as with quality. Mentor. Well then, Prodigy, what specifically have you in mind for your venture into futurism? Prodigy. I want to keep focused on Jim Boyd's concerns. When economic polarization develops along racial and color lines, it becomes singularly conspicuous and volatile. Affirmative action can ameliorate up to a point, but it also worsens tensions by breeding resentment. Mentor. Might it not help to develop a measure of polarization that could be expressed as a function of the population mix? Prodigy. I have developed such a function, which I will unveil shortly. But first allow me a few observations. Economic polarization is usually defined in terms of income or asset differences between haves and havenots. In the US the haves are whites and Asians; the havenots are blacks and browns. Unlike comparing rich with poor, not all whites and Asians do well and not all blacks and browns do poorly. Consequently, I decided to look at these two groups in terms of their statistical properties. Members of racial and ethnic groups, irrespective of individual economic success, very much identify with others of their tribe. They are bonded by primal survival instincts. It is human nature. When blacks and browns look through their "group eyes," they see whites and Asians as belonging to advantaged tribes. Racial and ethnic self-identification creates resentment even among successful individuals within the group. Success of other groups is seen as inherently unfair, because havenots operate from an equal-outcome perspective. They do not acknowledge inherent group differences, let alone their economic consequences. Alternatively, whites and Asians see jobs obtained by less qualified minorities as unfair, because haves operate from a meritocratic perspective. This difference in perception, stemming from divergent abilities, is at the root of intergroup resentment. Mentor. Can policies be enacted to reduce intergroup antipathy? Prodigy. Not the kind I speak of. What I describe is fundamental polarization, arising from inherent group differences. Government sponsored policies like affirmative action can act in behalf of blacks and browns. Employment measures can steer minorities into public sector jobs, creating a minority middle-class. Pressure on the private sector can achieve much the same effect. But none of this gets at the irreducible minimum intergroup resentment. Resentment is a two-way street. It exists both at the top and bottom. For a given racial/ethnic mix, government or private-sector intervention merely shifts resentment from one group to another. It is as if there were a conservation of resentment principle operating. In a meritocratic culture all the resentment is from the bottom. Chopping away at the meritocratic ideal by introducing equal-outcome components like affirmative action reduces resentment in one group, shifting it to another. Mentor. Can the level of ill feeling increase beyond the irreducible minimum? Prodigy. Absolutely. Race hustlers make a living by playing upon these antagonisms. I consider here, however, only the primary antipathy and its offshoot polarization. To study the effect of racial and ethnic composition on social discord, I developed a measure of intergroup polarization that is independent of government policy. Income and asset differences are inappropriate measures, because they are very much influenced by policies such as affirmative action. My measure of polarization is invariant to political perturbations, being instead intrinsic to the nature of the groups and their relative numbers. In fact, I call it the intrinsic polarization function. It describes the irreducible minimum intergroup polarization. On the human evolutionary scale, 50 or 100 years mean very little. Some human attributes change so slowly, that on this scale we may regard them as constant. Group-cognitive differences are among them. Having taken so long to shape, they will likely exist 50 years hence in the same form we observe now. Barring widespread intergroup breeding, these differences will persist. Asians and whites will remain as a cognitive elite, with blacks and browns lagging behind by about one standard deviation. Other group properties will likewise resist change. These simple facts allow me to frame the question of polarization in more concrete terms. And, being cautious by nature, I will make no extravagant claims. My foray into futurism will be more like a "what-if" game. Mentor. And of course you will not contradict any known facts. Prodigy. Of course. I propose a very simple model based on group-differential ability to earn. For this purpose, the US may be modeled as a two-group nation, blacks and browns in one group, Asians and whites in the other. The groups differ in a property we might call, earning ability. It is distributed differently within each group, the black/brown distribution lagging behind that of whites and Asians. Mentor. You mentioned time-invariant cognitive differences. Is there a relationship between earning ability and IQ? Prodigy. We know the two are strongly correlated. In fact, IQ is the biggest single correlate of income. That, however, is not to say that earning ability and IQ distributions are identical. They are not. Athletes and dentists, for example, have high-earning potential, yet at the same time can be dumb as rocks. However, barring profound changes in Western values, earning-ability gaps should remain fairly constant. Though the distributions of earning ability and IQ differ, the degree of correlation suggests they share some common elements. Intergroup gaps in both distributions should be similar. We know the IQ gap between blacks/browns and whites/Asians is about one standard deviation. Consequently, I assume throughout a one standard deviation earning-ability gap. Ultimately, however, the gap must be regarded as an adjustable parameter, and may be reset when evidence warrants. Mentor. You mentioned an intrinsic polarization function. Tell me about it. Prodigy. Within the context of the two-group model, I look at the proportion of blacks and browns in the top-earning quintile (more generally, n-tile). I brought some posters to help me explain. Poster 1 shows a utopian equal-outcome ideal in which the black/brown fraction of the top-income quintile equals the black/brown fraction in the workforce. In Utopia, earning-ability gaps do not exist.
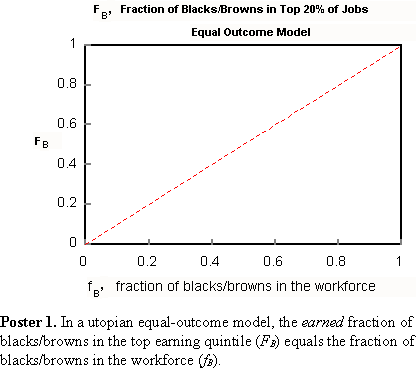
Poster 2 includes also the fraction of blacks and browns in the top-earning quintile that would obtain in a meritocracy, that is, when the quintile is filled in rank order of earning ability. Because of the earning ability gap, the meritocratic top-quintile fraction of blacks and browns, FB, is always less than the corresponding utopian fraction, fB. (See Poster 5 for how to calculate FB.)
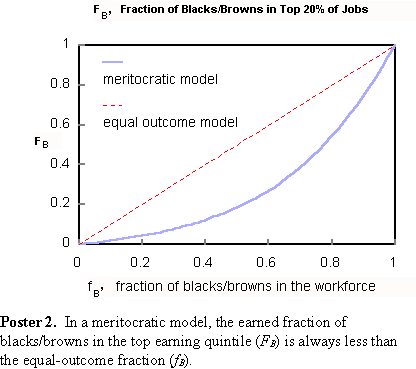 I define the intrinsic polarization function, p as the difference between the utopian and meritocratic curves. That is, p = fB - FB. The intrinsic polarization function depends only on a population's racial/ethnic makeup. It arises from deep-rooted group differences and has nothing to do with government or private-sector policy. Poster 3 shows how the function varies with the population mix. 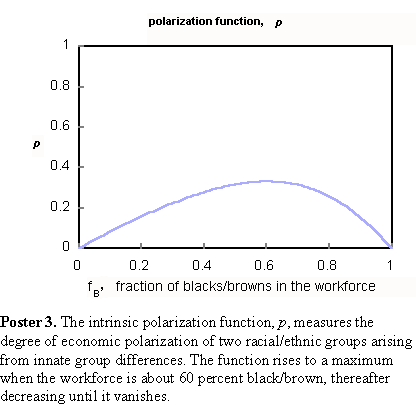 At the population extremes (no blacks/browns and all blacks/browns) the polarization function vanishes. Consequently, there must be a racial/ethnic mix where the difference reaches a maximum. This occurs when the workforce is about 60 percent black/brown. That is the most volatile mix. Further increases in black/brown percentages will see a decrease in polarization. Mentor. Where are we presently on your curves? Prodigy. In Poster 4, the 1999 black/brown workforce fraction (about 23 percent) is marked. The 1999 population mix
generated significant polarization, the intrinsic polarization function
reaching 53 percent of its maximum value. 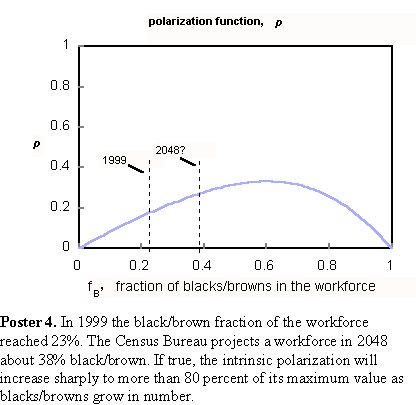 Circumstances degenerate as the workforce becomes more black and brown. The Census Bureau forecast of a 38 percent black-brown workforce in 2048 is also marked on Poster 4. At that mix, the intrinsic polarization function will have increased to more than 80 percent of its maximum value, a dangerous condition. The level of resentment will be way up. As Jim Boyd suggests, that combination of polarization and political muscle could produce destabilizing unrest. Mentor. How will the resentment be distributed between the two groups? Prodigy. My model cannot say. That would depend in large measure upon the existence and vitality of policies promoting concepts like affirmative action, "diversity," "multiculturalism," and others I can't even begin to imagine. Mentor. Though your analysis is well constructed, Prodigy, your conclusions are not quite as dramatic as the starvation of 65 million Americans in a decade. Prodigy. That's the price of circumspection. OK, so I won't get a MacArthur Award. Actually, my long-term outlook is fairly optimistic. If we can hold on long enough, the world will create so much wealth that economic polarization will become a moot issue. The problem is one of time scale. That is, how long is "long enough?" Meanwhile, let me show you how I evaluated the top-quintile earned fraction, FB, and the intrinsic polarization function, p. Please look at Poster 5.
POSTER 5. CALCULATION OF FB, THE EARNED FRACTION OF BLACKS/BROWNS IN THE TOP
QUINTILE, AND p, THE
INTRINSIC POLARIZATION FUNCTION.
Suppose a population, N, consists of two groups, the black/brown numbering NB and the white/Asian numbering NW. We wish to fill N/n slots in rank order on some property, x, where 1 < n < N. Let P(x) be the probability density of x in the white/Asian group. Let the probability density of x in the black/brown group be P(x + Δ). That is, the two distributions differ by a translation, Δ, along the x axis. The quantity, Δ, is the difference between the group means. Then, the following relation is satisfied (see Women and Minorities in Science).
Members of the population possessing a value of the property greater than or equal to λ make the cutoff and fill one of the slots. The first term on the left side (5.1) is the number of whites/Asians who fill slots; the second term is the corresponding number of blacks/browns. Dividing through by N/n, the number of slots in the top n-tile, we get
In (5.2) we have replaced NB/N with fB, the fraction of the general population that is black/brown. The value of λ is determined in practice by numerical solution of (5.2). The second term on the left side of (5.2) is the earned fraction of blacks/browns in the top n-tile, i.e., FB. The intrinsic polarization function, p = fB - FB, is then given by
The functions FB and p were evaluated throughout for Δ = 1 and n = 5, i.e., for the top quintile. Mentor. Straightforward enough. Is there more? Prodigy. The intrinsic polarization function and earned fraction of blacks/browns have interesting limiting properties, which I have formulated into a pair of limiting laws. I call them Prodigy's Laws. Mentor. Not surprising. Prodigy. The laws provide considerable simplification in low brown/black populations. They would apply very well in, say, the UK. Please look at Posters 6 and 7.
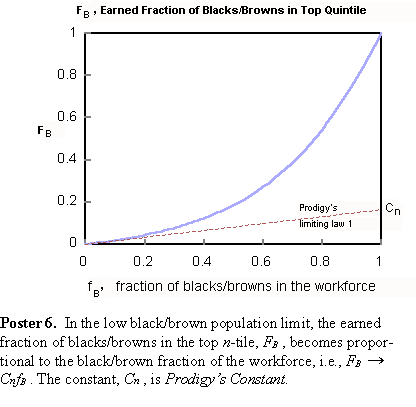 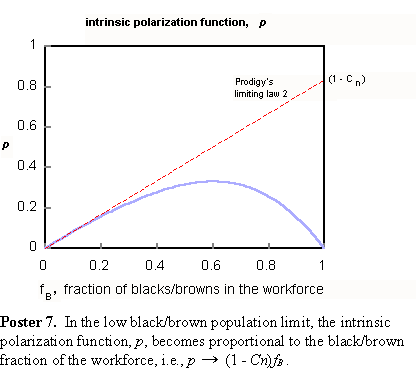
As you see, Mentor, both the earned fraction, FB, and the intrinsic polarization function, p, approach asymptotes in the low
black/brown population region. Their limiting behavior forms the basis of Prodigy's
laws. I develop them in Poster
8.
POSTER 8
Prodigy's Law I can be obtained by expanding FB (fB ) about zero and dropping quadratic and higher terms,
where λ(fB) is the smallest value of x that earns a slot in the n-tile. From (8.2) we can find FB' (fB):
To find FB' (0), we note that the derivative in (8.3) expands to -P(λ+Δ))(dλ/dfB), both factors of which remain finite as fB 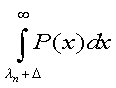 , where λn is the value of
λ in an all-A population competing for slots in the top n-tile. That value of λ
satisfies the relation: , where λn is the value of
λ in an all-A population competing for slots in the top n-tile. That value of λ
satisfies the relation: 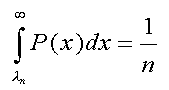 , which also provides a means to compute λn. Thus, FB'
(0) is given by , which also provides a means to compute λn. Thus, FB'
(0) is given by
and Prodigy's Law, F(fB) = CnfB, is established. Prodigy's constant, Cn, is also seen to be F' (0) or 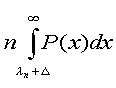 .
Values of Cn can be computed from this expression. .
Values of Cn can be computed from this expression.
A few values of Prodigy's constant are tabulated below, for the case when P(x) is Gaussian and Δ = 1.
Prodigy's Law II follows directly, since p = fB - FB
Mentor. Does Prodigy's constant have any significance? Prodigy. "Significance" is a bit strong, Mentor. Will you settle for "interpretation?" Prodigy's constant is the earned top n-tile fraction of blacks and browns in a hypothetical all black/brown population that obeys Prodigy's Law I over the entire range of population mixes. Mentor. Yes, I do think "interpretation" is more appropriate. Have you considered the tendency of minorities to cluster geographically in cities? Prodigy. I am looking into that. Oops, please excuse me, I am late for an appointment with Aunt Patricia. She promised to lend me a copy of Lowell Ponte's "The Cooling." Mentor. I look forward to our next meeting. Prodigy. Me too. Thanks for the lesson and the cookies. |
|||||||||||||||||||||||||||||||||
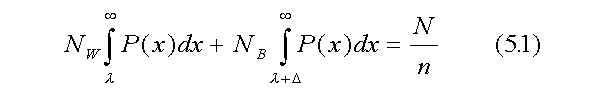
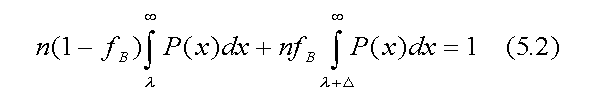
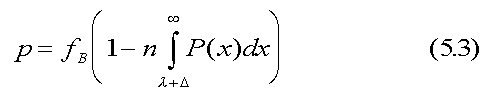
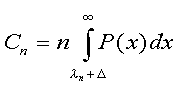 , where
λn is the solution of
, where
λn is the solution of 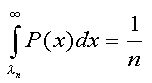 . The quantity,
P(x), is the distribution function of property x for group A. The distribution function for group B is P(x +
Δ).
. The quantity,
P(x), is the distribution function of property x for group A. The distribution function for group B is P(x +
Δ).