Volume 1,  Number 1
September 1999  

Prospects for women and minority doctoral scientists in engineering and other math-intensive areas are examined. A calculation of the ethnic-gender profile of this segment of the workforce is made for U.S. citizens and permanent residents. Rank ordering on mathematical reasoning ability predicts that women will top off at approximately 27 percent of this market. Similarly, rank ordering predicts almost 99 percent of math-intensive doctoral jobs will go to whites and Asians of primarily Chinese, Japanese, Korean and South Asian descent. Asians will continue to be represented in these fields well beyond their numbers in the general population. A study of the math-intensive academic marketplace predicts that women will top off there at about 22 to 23 percent. 

From the University of Texas we read: 

"Diversity derived from inclusion of all groups is essential for solving the engineering challenges of the 21st Century. Women are a vital human resource for this endeavor. The Women in Engineering Program is an agent for intervention and a catalyst for transformation."

"A scholarship fund endowed by your corporation would be a major help in attracting women to Rensselaer. A scholarship of $5,000 per year for four years would allow your company to sponsor a Rensselaer scholarship named after your corporation."

"As part of a leading education and research institution in the nation, the College of Engineering at Georgia Tech will provide an environment conducive for women to pursue successfully and in a professional manner an engineering education and career."

Graduate schools are also swept up in the gender-equity game. A movement to increase graduate degrees among women in engineering and science is vigorous and widespread. These efforts have substantially narrowed the numerical gap between men and women new PhDs. Women currently account for more than 45 percent of new PhDs in the biological sciences. Attempts in the more mathematically based disciplines have been less successful. 

We isolate four technical fields that lean heavily on mathematical aptitude: engineering, physical science, computer science and mathematics. These disciplines span the math-intensive areas. The gender gap there is more resistant to closure. How much narrowing can we expect? Will women ever be proportionally represented in these technical fields? Will encouragement, financial incentives and admissions chicanery be enough to eliminate the gap? We will address these issues here. 

Evidence points to a gap between men and women in mathematical reasoning ability. Men seem to have the edge. Though statistical in nature, the gap is sufficiently large that most people suspect it simply from their life experience. Evidence, however, raises the issue above the level of suspicion. Simply put: On all standardized exams, including IQ tests, men score higher than women on mathematical reasoning sections. The effect crosses all races and cultures. It may be biological or environmental in origin, but that is another issue. We merely note that all efforts to erase the math gender gap have failed. 

In a bias-free employment market it is possible to calculate the maximum proportion of women that we can expect to be employed at the doctoral level in the collective areas of engineering, physical science, computer science and mathematics. We will gauge the efforts of government, industry and universities against the results of this calculation. 
 

DEFINING THE GAP 
The math gap is ubiquitous, and can be assessed from as simple an instrument as the Scholastic Assessment Test (SAT). For many years boys have outperformed girls on the mathematical reasoning part of this exam. After small gains by women, the difference in performance leveled out and has remained remarkably constant for years. The gap persists, not withstanding that girls get better grades in school and despite considerable efforts to bring the male and female averages together. Figure 1 shows eleven years of Math SAT averages for men and women. Both sexes show a general upward trend from 1984 through 1994, but the male - female difference has remained almost constant. 

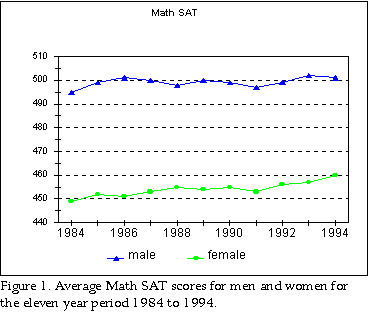In 1998, more than a million college-bound high school seniors took the SAT I mathematical reasoning test, 541,962 men and 630,817 women. Men averaged 529.6 (SD = 114.1). Women averaged 494.5 (SD = 107.8). Since the two distributions have slightly different standard deviations, we computed the gap as the difference in the means divided by the root mean square of the two SDs, obtaining a male-female math gap of 0.32 SD. 

Math SAT scores range between 200 and 800. (You get 200 for writing your name.) Contrary to popular belief, 800 is not a "perfect score." It simply means that some threshold has been reached. Two students, each with scores of 800, will not necessarily have done equally well. A few years ago the College Board changed its scoring system. They called it "recentering." Ostensibly, recentering was designed to bring both the verbal and mathematical averages closer to 500. There were, however, other only rarely mentioned consequences. Recentering compresses the distribution of scores near the top, so that the best students become difficult to distinguish from one another. The new scoring system blurs the line between excellent and exceptional. Truly special students get lost in the crowd of very good students. In the year just before the SAT was recentered, 32 students nationwide scored a "perfect" 1600 on the combined math and verbal exams. The following year, after recentering, 545 students scored 1600, about 17 times more than under the old system. Coincidence or not, recentering is part of a leveling process in education, which attempts to minimize differences between students. With recentering, high scorers cluster together near the top of the distribution, making it easier for very selective schools to justify admitting more minorities. The SAT no longer distinguishes high-scoring minorities from higher achieving Whites and Asians. Nonetheless, despite all these limitations the SAT remains an extraordinary tool. 

Only about 30 percent of youngsters who are high school senior age take the exams. They are not representative of American youth. More girls than boys take the exams. Some students headed for college take the American College Testing Program (ACT) exams rather than SATs. Others who do not take SATs have taken themselves out of the college marketplace. Some have dropped out of school. For all these reasons SAT takers are not representative of their age group, and plausibly we might be  criticized for using SAT results to assess a general gender difference. Addressing this problem, we can infer from a few mild assumptions the distributions of SAT scores that would be obtained if every person in the country of high school senior age took the exam. 

Most of the brightest students take SATs, even those from ACT states. A senior in an ACT state who is even thinking of applying out of state, will take SATs. Thus, we can assume with little error that just about all the brightest youngsters in the age group will take SAT exams. They will place in the high-end tail of the distribution. Consequently, the high end region of the curve will look more-or-less as it would if every last person in the age group took the exam. From the characteristics of the high-end tail we can reconstruct the full distribution as it would look for the entire high school senior age population. 

Let P_M(x)dx be the probability of a male obtaining an SAT score between x and x + dx. Let P_F(x)dx be the corresponding probability for a female. (The quantity, x, is in SD units.) Now suppose that each of the two distributions is Gaussian, with equal standard deviations. Further, the distributions are displaced from one another by a gap, Δ, such that: 
 

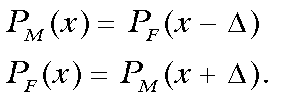                                         (1)

The quantity, Δ, is the difference between the mean scores, male - female. 

Let f_M and f_F be the fractions of males and females who obtain the score, l, or better. Then, 
 

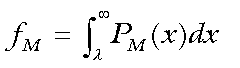                                            (2)

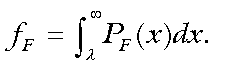                                             (3)

For convenience, we note the following transformation: 

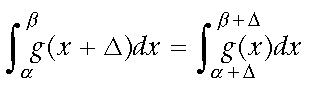                                 (4)

and write for f_F, 
 

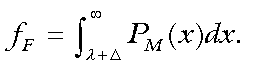                                      (5)

In 1998, 0.765 percent of the entire resident population of male 17-year-olds in the U.S. took the SAT math exam and scored 750 or higher, compared with 0.318 percent of the corresponding females. That is, f_M = 0.00765 and f_F = 0.00318 for λ (in SD units) equivalent to a 750  SAT score. Further along the tail, 0.430 percent of the resident men in this age group scored 780 or better, compared with 0.164 percent of the corresponding women, i.e., f_M = 0.00430 and f_F = 0.00164 for λ equivalent to a 780 SAT score. We can be confident that both rarefied groups contain just about all of the nation's most mathematically talented 17-year-olds. 

From these data we can obtain the difference between male and female means for the entire age group. Assuming a normalized Gaussian probability density centered on zero, (2) may be solved numerically for λ, the number of standard deviations the threshold score is displaced from the mean score of P_M. For a score of 750, we find λ = 2.43; for a score of 780, λ = 2.63. Knowing λ, (5) may be solved numerically for Δ, the gap between the male and female means. The 750 cutoff yields Δ = 0.303, and the 780 cutoff returns the value Δ = 0.313. Both results are remarkably close to the gap of 0.32 SD observed from the group of just test takers. We will use the value, Δ = 0.31 SD. 
 
According to the 1995 Survey of Doctorate Recipients published by the National Science Foundation, that year 181,800 doctoral scientists were employed as mathematicians, computer scientists, physical scientists and engineers. In 1995, women made up 9.7 percent of this workforce. If the 181,800 slots were filled strictly according to mathematical aptitude, a different proportion would have emerged. We solve a rank order problem to find that proportion. 

Suppose N_S slots are to be filled in order of ability from a pool of N_M men and N_F women. Assuming a distribution of ability, all those with ability equal to or greater than some value, λ, will be selected to fill a slot. The cutoff ability, λ, can be determined from the pool sizes, the number of slots available and the ability distributions for men and women. The variables are related as follows: 
 

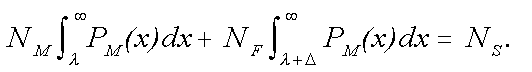(6)

The first term on the left side of (6) represents the number of males who make the cutoff; the second term is the corresponding number of females. The two terms add up to the number of slots, N_S. From the pool sizes, N_M and N_F, the number of available slots, N_S, and the gap between the male and female distributions, Δ, we may find the cutoff ability, λ, by solving (6) numerically. Knowledge of λ allows evaluation of the first and second terms on the left side of (6) giving the number of men and women, respectively, selected to fill the slots. 

For N_S = 181,800, the number of doctoral scientists employed in math-intensive areas in 1995, we calculated the expected percentage of females, assuming the slots would be filled in rank order of mathematical ability. The calculation proved not very sensitive to pool sizes so long as the ratio of men to women remained essentially constant. We formed the pools from men and women between the ages of 25 and 65, using 1996 population data. In this age range there were 68.7 million men and 70.8 million women resident in the U.S. in 1996. The quantities, N_M and N_F, were set to these values, respectively. The resulting calculation predicted that female doctoral scientists will saturate the math-intensive marketplace at approximately 27 percent. 

Conclusions 
The 1995 figure of 9.7 percent women doctoral scientists in math-intensive fields leaves lots of room for increased participation before the predicted limit kicks in. Many of these women entered the workforce years ago, before the drive to get women into the sciences, so we should look for an increasing female presence over the next few years. Across the fields of engineering, mathematics, and physical and computer sciences, there is wide variation in the representation at the doctoral level by women. In 1995 for example, at the doctoral level women made up 11.7 percent of physical scientists, 10.6 percent of computer scientists, 4.9 percent of engineers and 17.7 percent of mathematicians. Overall, 9.7 percent of the doctoral scientists in these areas were women. Thirty years ago, women were so poorly represented in the highest levels of the technical workforce, that they were all but invisible. Since then, they have made enormous gains, but are still underrepresented, especially in engineering. They have come a long way, but will soon run into a statistical barrier, penetrable only by political or social intervention. Looking at recent doctoral recipients, we get a sense of the workforce of the future. In the combined areas of physical science, mathematics, computer science, and engineering, women earn more PhDs than before. In 1983 only 10 percent of these degrees went to women. By 1988, the proportion was up to 14 percent. More recently, the 1995, 1996 and 1997 numbers were up to 20.5, 19.3 and 19.8, respectively. Room for further increases still remains before the ladies bump up against a statistical ceiling near 27 percent. 
 

SUPER ELITE WOMEN 
Among doctoral scientists, a more elite segment may be found. They are the faculty of research universities. An academic department in a research university is like a ball club. Faculty members push the envelopes of their research to enhance their reputations, but they also like to be on a winning team. Building the department's reputation is important. The department's appetite for talent is insatiable. When a position opens, a search is launched worldwide to attract the best person. The academic marketplace is matched only for dog-eat-dog aggressiveness by major league sports. 

When finally appointed, a new junior faculty member must hit the ground running. He has a six year contract, but in reality he has only four and a half years to prove himself. A tenure decision will be made in the middle of his fifth year. It is the most critical time of his life. He has been preparing for this moment since he was an undergraduate. After the B.S., four or more years in graduate school, at least two years of postdoctoral training in another laboratory, and he is ready to fly on his own. Four and a half years later he will come up for promotion and tenure. It is up or out. Failure to get tenure means he must leave the university. If he fails, he will have the remaining year and a half of his contract to find a new job. Though publicly denied, in practice the candidate will be judged solely on the research criterion. It is a fair system because both the candidate and the department understand the rules from the outset. 

In the short time the candidate has been at the university, he is expected to have attracted independent funding, to have produced significant research output, and have established a national reputation in his field. A committee of peer plus department members and at least one outsider will decide his fate. Often students are included to help with the evaluation of teaching. However unless the candidate is a basket case in the classroom, he will satisfy the teaching criterion. The evaluation turns primarily on the assessment of outside referees, the most renowned investigators in the candidate's field. Each is asked to evaluate the candidate's work, with which they should already be familiar. The fundamental question is whether this candidate, in the past four plus years has done the quality work expected in academic research. If the answer is yes, the candidate will be advanced to tenure and promotion. Characteristically, about half the candidates make it. The elite group of academic scientists who obtain tenure represents the cream of American science. We ask at which point this market will saturate with women? 

To obtain the number of available slots in our rank order game, we must count the tenured faculty who work in math-intensive disciplines in American research universities. We can make a ballpark estimate of their number by looking at a product of their labors: new PhDs. For the last few years our universities have been turning out twelve to thirteen thousand PhD scientists a year in the math-intensive fields. Most are produced by senior faculty. Assuming an average of one new PhD per year per tenured faculty member, we estimate the number of slots to be 12,000 or so. The calculation proves only mildly sensitive to slot size, making the ballpark estimate sufficient. 

In the math-intensive areas, what is the fraction of tenured research-university faculty that we can reasonably expect to be female? Equation (6) again provides the answer. For a gap, Δ = 0.31, slot sizes, N_S, between 8,000 and 17,000 (bracketing our ballpark estimate) and pool sizes, N_M and N_F, taken as the populations in the 25 to 65 age bracket, we predict that women will saturate this academic market at between 22 and 23 percent. With fewer slots available, women do not fare quite as well. Table 1 summarizes the results. 

MINORITIES 
The College Board groups SAT takers into several ethnic categories. The groups include American Indian or Alaskan Native; Asian, Asian American or Pacific Islander; African American or Black; Mexican or Mexican American; Puerto Rican; other Hispanic and White. The Asian/Pacific Islander designation is particularly troublesome because the facts suggest that within this category are very disparate groups including the very bright and the very dull. In fact, the 1990 census shows that the Asian/Pacific Islander category for SAT purposes includes Chinese, Filipino, Japanese, Asian Indians, Koreans, Vietnamese, Cambodians, Hmong, Laotian, Thai and other Asians. Also included are Pacific Islanders, which further subdivide into Polynesian Hawaiians, Samoans, Tongans, other Polynesians, Micronesians, Guamanians, Melanesians and unspecified others. Out of these, 48 percent are Chinese, Japanese or Korean, the troika of high achievers. 

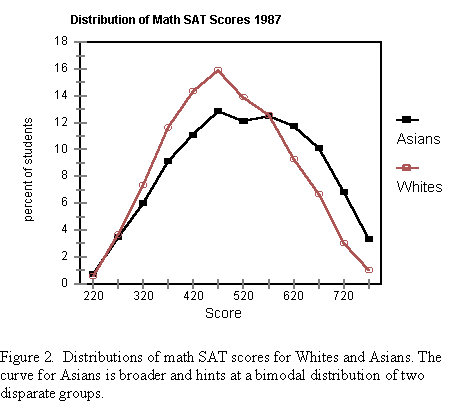
All the groups designated by the College Board have math SAT distributions with standard deviations clustered about 100, except the Asians/Pacific Islanders. And no wonder. Their standard deviation is closer to 120, showing their diverse nature. The distributions for 1987 for both Asians and Whites are shown in Figure 2, where the qualitative difference between the two distributions is apparent to the naked eye. The distribution for Asians is uncharacteristically broad, with a flattened top. It hints at bimodality. 

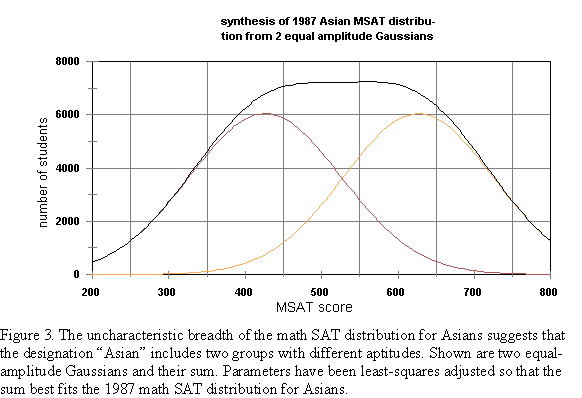
An attempt was made to fit the "Asian" MSAT distribution for 1987 and 1992 (the years for which we had access to the ethnic distribution data) to a sum of Gaussians. Since the elite Chinese, Japanese, Koreans and South Asians made up about half this group, the Gaussians were given equal weight. (See Figure 3.) The least-squares fit suggests that this Asian quartet performed with a mean of approximately 627 for 1987 and 641 for 1992. The remaining Asians had mean scores of approximately 426 (1987) and 444 (1992), not unlike American Indians. Choosing Whites as the reference group (Δ = 0), and averaging over both years yielded Δ = -1.24 for elite Asians, and 0.47 for other Asians. Other group Δ's were obtained from 1998 MSAT mean scores as follows: Hispanic = 0.683, Black = 0.99, and American Indian = 0.437. A rank order analysis, similar to that used for the sexes, was performed using an extension of (6): 
 

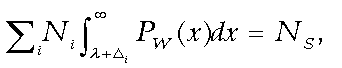                 (7)

The number of slots, N_S, was set equal to 181,800, the number of doctoral scientists employed in 1995 in the selected technical fields. Again, we used the 25 to 65 age range for the pool numbers, this time for each racial or ethnic group. We allowed for multi-talented people to choose completely different fields by cutting the pool sizes for each group proportionately and incrementally from the full populations down to 1/5 of the full pool. The resulting predictions thus fall into ranges. They are summarized in Table 2. For comparison, we also show the percentage of doctorates actually awarded to U.S. citizens and permanent residents in the selected fields in 1995. 

 

	Percentage of doctorates awarded in math-intensive fields in 1995 (by ethnicity)	Predicted percentage (by ethnicity) of doctoral positions if filled by rank ordering on ability,
Whites	66.1	59 to 72
Asians and Pacific Islanders	28.1	26 to 40
American Indians	0.28	less than 0.2
Hispanics	2.3	0.6 to 1.1
Blacks	1.7	less than 0.5
unspecified	1.5
Table 2. Predicted percentages, by race and ethnicity, of jobs filled by doctoral scientists in math-intensive fields if filled in rank order of mathematical ability. Also shown, for comparison, are percentages of doctorates awarded in these fields in 1995 to U.S. citizens and permanent residents.

 

Conclusions 
La Griffe predicts that the PhD market in the math-intensive technical areas will saturate at almost 99 percent White and Asian. Of the Asians, almost all will be either Chinese, Japanese, Korean or South Asian. Whites will fill 59 to 72 percent of the jobs, Asians: 26 to 40 percent. Asians will continue to be represented well beyond their proportion in the general population. Black and Hispanic PhDs in the selected areas are being turned out at a slightly higher rate than we predict. However, the difference is within the error of our calculation. We should expect that the future will see Whites and Asians to continue to dominate this segment of the job market, to the virtual exclusion of other groups. The close agreement of doctorate production by race and ethnicity with the predicted proportions of job holders suggests that the marketplace, at least for now, has reached a steady state essentially free of external influences.
 

Population by Age and Sex 1990 - 1999 

Population by Age, Sex and Ethnicity 1996 

SAT Means by Sex, Race and Ethnicity 1984 - 1994 

SAT Means by Race and Ethnicity 1998 
  
SAT Distributions 1998