According to Kevin MacDonald, Judaism is a group evolutionary strategy, a thesis well supported by this morning's bagels and whitefish. The nova provides further evidence that Judaism is a complex of adaptations leading to evolutionary success. But I come this morning to speak not of lox but rather of intelligence, in particular the intelligence of the Ashkenazic Jew.

    Many of you at this breakfast table are exemplars of Ashkenazic success as evidenced by the abundance of Jaguars and Mercedes in the parking lot. (They did not go unnoticed by my mother when she dropped me off.) But these symbols of your accomplishment do not reflect the kind of success I will talk about today. Instead, I shall focus on Jewish achievement that links more obviously and directly to cognitive ability.

    Ashkenazim have earned 27% of the Nobel Prizes awarded to Americans, 25% of ACM Turing Awards, and 26% of the Fields Medals. They account for more than half the world chess champions. Ashkenazic Jews, 2 percent of the US population, make up 30% of elite-college faculty, 30% of Supreme Court law clerks, and 27% of Ivy Leaguers. In my lecture this morning I will demonstrate how from such data the Ashkenazic IQ can be revealed.

    Psychometricians agree that Ashkenazim are smarter than other Europeans. By how much, however, is not settled. Estimates vary mostly because of problems with sampling. I have seen assessments of the mean Ashkenazic IQ from 107 to 117, a spread of two-thirds of a standard deviation. Finding this discrepancy profoundly unsatisfactory and thoroughly disagreeable, I undertook to appraise for myself the Ashkenazic IQ. And because psychometricians cannot agree, even among themselves, I approached the problem de novo, paying no attention to their methods or to their results. I avoided their sampling difficulties by considering populations of entire nations and continents. But, I am getting ahead of myself.

    The method used is due to La Griffe du Lion. It was introduced in his essay, Aggressiveness, Criminality and Sex Drive by Race, Gender and Ethnicity. The procedure enables the determination of group mean differences from the differential rates at which groups cross certain behavioral thresholds. Appropriately, La Griffe termed it the method of thresholds.

    In the present application several conditions must be met:

1) A threshold of performance must be found that depends purely on cognitive ability.

2) The threshold must be unequivocally defined.

3) The rates at which Ashkenazim and other whites cross the threshold must be established.

4) Opportunity must exist for both Jew and non-Jew to cross the threshold. That is, Jews cannot be restricted by political considerations from fair competition.

5) An overriding motive to cross the threshold must exist, being sufficiently strong that virtually all those capable of crossing the threshold do.

    One by one, I reviewed areas in which Ashkenazim excel, and one by one I rejected them. Overriding motive was the most difficult standard to meet. Many people, for example, match the intellectual capability of a Supreme Court clerk, but may choose to be stock brokers or physicians or do science instead. There is no overriding motive to be a lawyer. In fact, the same may be said of almost every activity where brains rule. It goes with the territory. Smart people have many options. Overriding motive does not come easily.

    I mulled over this problem for several days, until one morning, as Mom packed my lunch for school, the answer struck me suddenly. In the former Soviet Union, the confluence of a failed economic system, totalitarian government and a specific national passion created a circumstance singularly suited to the determination of the Ashkenazic IQ. Out of this joyless society materialized the data required for the calculation. The Soviets had fashioned a threshold that met all the conditions I had imposed, to wit: eligibility to play in the annual USSR Chess Championships.

    Permit me a brief digression. Contrary to what some believe, most great chess players are not geeks.  A look at their lives reveals an enormous array of occupations, some rather improbable. The nineteenth century grandmaster Max Harmonist, for example, earned a living as a ballet dancer. We find among the ranks of chess masters, lawyers, accountants, engineers, dentists, psychologists, priests, Shakespearean scholars, musicians, scientists and more. The single thread tying great players together is intellect. Chess ability is very much a product of general intelligence.

    In the former Soviet Union (as today in its remnants) chess was a national obsession. Great chess players were accorded enormous respect. While ordinary Soviet citizens struggled to maintain a bleak existence, grandmasters led lives of relative privilege, even gaining some measure of wealth. By Soviet standards they were rich.

    The success of Soviet chess is without parallel. In 1927 Alekhine defeated Capablanca to become the first Soviet world champion. From the time of Alekhine's victory, there have been only five years with a reigning world champion born outside the Soviet Union. In this nation, where every child plays chess, every citizen had both opportunity and motive to hone his chess-playing ability to its keenest edge. If ever there existed a place where latent chess talent had to be discovered and nurtured it was the USSR.

    Participants in a USSR Championship tournament typically numbered about 20. They represented the cream of Soviet chess. The right to participate was a cognitive threshold that met all my requirements. I lost no time gathering data for my calculation. A web search quickly produced the complete record of USSR Championship tournaments for the years 1947, 1948, 1949, 1970, 1971, 1972, 1973, 1974, 1975 and 1976. 

    At the risk of wearying an audience that has not yet digested its breakfast, I think it necessary for me to explain a bit about the input required by the method of thresholds. The fractions of Soviet Jews and non-Jews who made the cut are needed. In the ten years for which I had data, the names of Jewish participants appeared 83 times, and non-Jews 110 times. The average number of Jewish and non-Jewish participants per year were thus 8.3 and 11.0, respectively. For these years Jews in the USSR numbered about 2 million in a population of approximately 230 million. Something like 1 in 21 million Soviets were good enough to play in a championship tournament. One in 240,000 Ashkenazim qualified. An Ashkenazi was 88 times more likely than a non-Jew to make this exclusive club.

    Raw population statistics are not best suited for the computation of the required population fractions. At this level of chess women are simply not competitive. Neither are children or elderly. Consequently, a base population for this calculation is better characterized by the total population minus women, children and geezers. A good approximation to this number is obtained by reducing a population to 25% of its original value. The method of thresholds, however, is very forgiving of this factor's precise size. Varying it from 20% to 50% produces less than a one point difference in the calculated IQ. I used the value, 25%, which, demographics suggest, is close to best.

The fat tail
    Qualifying for a USSR championship tournament guaranteed an IQ way out on the IQ curve. In such rarefied cognitive territory IQ distributions deviate significantly from normality. Many more high-IQ people are observed than predicted by a Gaussian distribution. The IQ distribution is said to have a fat tail. Participants in the Soviet chess championships were so bright this fat tail could hardly be ignored.

    In a classic study of giftedness, launched in 1921, Lewis M. Terman documented the frequency with which high IQs occur. Though only ancillary to his study, the frequency data is, in my opinion, its most important result.

    I constructed a function to fit the high-IQ data of Terman. In addition to fit, I required the function to meet two other criteria: 1) I wanted it to "look like" a bell curve in regions of moderate IQ, and 2) I required it to be normalizable. The addition of low-amplitude Gaussians, each with unit standard deviation, to the wings of the bell curve did the trick. (To preserve the function's symmetry, I added the terms symmetrically on each side of the maximum.) The resulting normalized function is given below:

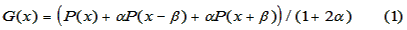
    In (1), P(x) is the standard normal distribution. The function, G, has two adjustable parameters; α scales the added terms and β locates them. The best fit to the Terman data was obtained with α = 0.01466 and β = 2.5469. I call the function (G) Griffe's function, an homage to La Griffe du Lion for his encouragement with this undertaking. Figure 1 shows the fit of G to the high-IQ data of Terman. At IQs greater than 5 standard deviations from the mean, the observed frequency of occurrence can be thousands of times that predicted by a normal distribution. 

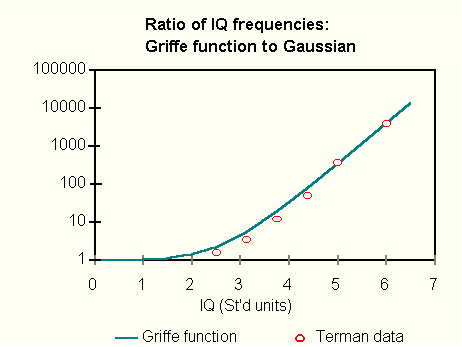
Figure 1.  The curve represents a ratio of the probabilities of exceeding a given IQ, viz. that computed from Griffe's function to that computed from a normal distribution. The open circles correspond to the data of Terman.

Figure 2 shows how the function, G, satisfies the condition of "looking Gaussian" over most of the observable IQ range.

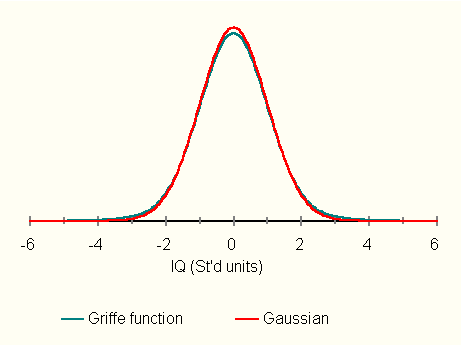
Figure 2.   Griffe's function differs minimally from a normal distribution at moderate IQs.

Figure 3 zooms in on the two functions to show how G deviates from a Gaussian at high IQs.

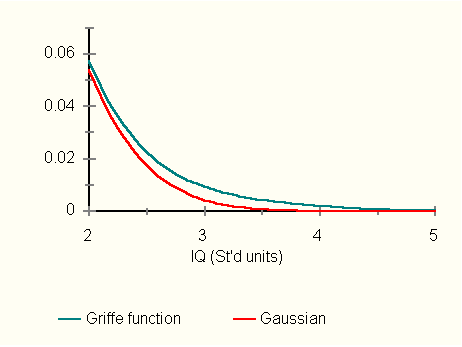
Figure 3.  Details of the normal distribution and Griffe function beyond 2 standard deviations.

    Crunching the numbers using Griffe's function (1) and the method of thresholds yielded from Soviet chess data a mean Ashkenazic IQ 1.06 standard deviations above the non-Jewish Soviet mean. Approximating the non-Jewish Soviet mean IQ by the Russian mean estimated to be 96 by Lynn and Vanhanen in IQ and the Wealth of Nations (2002) yields an Ashkenazic IQ of 112.

Mathematical IQ
    The second part of my lecture this morning deals with a peculiar aspect of Ashkenazic intelligence. Psychometricians find that Ashkenazic IQ is strongest on the verbal side. Ashkenazim, however, have contributed impressively in areas not obviously dependent on verbal skills. They produce great mathematicians as well as great lawyers. I sought to obtain an assessment of Ashkenazic mathematical ability, or if you like, the Ashkenazic "math IQ." Though math IQ may be related to what psychometricians call "performance," they are not one and the same. Math IQ reflects a creative ability peculiar to mathematicians and a few others like theoretical physicists. It is not so much the ability to stand out on WAIS-III IQ performance scales, but rather to go boldly where no man has gone before.

    To assess the Ashkenazic math IQ, I needed a purely mathematical threshold, one that satisfied the 5 conditions laid out earlier. The Fields Medal came immediately to mind. It is perhaps the highest honor bestowed upon a mathematician today. The special intellect required to produce mathematics worthy of a Fields Medal cannot be concealed. It will emerge and with virtual certainty be recognized.

    Established in the will of John Charles Fields, the first medals were awarded in 1936. They were suspended during WWII, not resuming until 1950. They have been conferred quadrennially since. Through 1998, Medals were presented in 14 years. Among the winners were 38 of European descent including 13 Ashkenazim. Thus, per year, among Western winners, there averaged 13/14 Ashkenazim and 25/14 non-Jewish whites. The fractions of Ashkenazim and non-Jewish Westerners among the winners, required by the method of thresholds, was computed assuming 13 million Ashkenazim and 1 billion non-Jewish whites. Because women are vanishingly inconspicuous at this level of achievement, and the medals are awarded to mathematicians no older than 40 years, the base populations had to be reduced. I applied a factor of 0.2 to these populations to reduce them to more appropriate values. Again, the method of thresholds is very forgiving in this respect, tolerating wide variations of the factor without much effect on the calculated IQ. Using Griffe's function and crunching the numbers produced an Ashkenazic math IQ of 111, 0.73 standard deviations above the non-Jewish white mean.

    About a month before I did this calculation, my friend Razib shared with me a list of competitors in the Putnam Mathematical Competition. Each contestant on his list had received at least honorable mention for the years 1994 through 2002. I thought Razib's list had the potential to provide another mathematical IQ threshold.

    For those not familiar with the William Lowell Putnam Competition, it is an annual event sponsored by the American Mathematical Society. It is also the premier mathematical competition for undergraduates in North America. Each year nearly 3,000 contestants from over 400 colleges and universities participate. Though it is an individual competition, a school may designate three entrants to represent it as a school team. Team scores are computed from the scores of individual team members. According to the Putnam announcement, "the first-place team receives an award of $25,000 and each member of the team receives $1,000. The awards for second place are $20,000 and $800; for third place $15,000 and $600; for fourth place $10,000 and $400; and for fifth place $5,000 and $200."

    There is a pecuniary motive to compete, but the Putnam is not about money. Even honorable mention  is a valuable addition to a curriculum vitae, not to mention the ego factor of receiving an award. Mostly, students with Putnam-level math ability have self-sorted by the time they enter college. Almost all enroll in powerhouse universities. The Putnam challenge will sweep up virtually all North American undergraduates who have a chance to place. Few truly mathematically gifted undergraduates escape its allure. All this considered, I decided to plug some Putnam numbers into the method of thresholds.

    Removing redundancy from Razib's list (Putnam competitors may enter in more than one year) I identified 325 distinct individuals who had received at least honorable mention. Razib had assigned race and ethnicity to the competitors based on their names. My independent assessment of ethnicity identified 51 Ashkenazim in the list. (Razib had identified 50.) Though our assignments disagreed a bit in the details, I was uncommonly pleased with the agreement of their bottom lines, so despite the difficulties associated with assigning ethnicity by name, I decided to give the Putnam list a run through my IQ engine.

    In the 9 years between 1994 and 2002, I estimated 191 non-Jewish whites and 51 Ashkenazim received at least honorable mention. Per year the average numbers of Ashkenazic and non-Jewish white honorees were thus 51/9 and 191/9, respectively. I again excluded women from the base populations (though a tiny few obtain some measure of success in the Putnam). Also, the competition is limited to undergraduates, which further constrains the pool of potential contestants. A four year span in the neighborhood of ages 18 to 21 includes about 5.5 percent of the US population. There were approximately 2.75 million Ashkenazic and 132 million non-Jewish white men in the US for the years included in the data. Appropriately, I reduced these numbers to 5.5 percent of their values for the calculation. Crunching the numbers yielded an Ashkenazic math IQ of 110, 0.68 standard deviation above the non-Jewish white mean.

    Recalling the Fields result of 111, 0.73 standard deviation above the white mean, it was with more than ordinary pleasure that I took notice of the outcome. Still, because assigning ethnicity by name is problematic at best, the Fields result remains the best value for Ashkenazic math IQ.

   The full implications of a 0.73 standard deviation may not be obvious to the casual observer. Suppose, for example, we compare the math IQ of a randomly selected Ashkenazic Jew to that of a similarly selected non-Ashkenazic white. Can you guess the probability that the non-Jew has the higher math IQ? It is 31%. That is, if you were to perform this selection experiment repeatedly, the non-Jew would come out ahead about 1 in 3 times. Add to this the fact that the business of ordinary living does not much depend on this ability and we conclude that a math IQ gap of 0.73 standard deviation would go mostly unnoticed except perhaps among university math faculties where a third or more Ashkenazim is commonplace.

    Though the implications of a 0.73 standard deviation gap may go unnoticed by the man in the street, they are profoundly evident at the highest levels of achievement -- the levels that leave a lasting imprint on civilization. Such a gap makes a random Ashkenazi Jew 40 times more likely to win a Fields Medal than a random non-Jewish white. In all, thirteen Fields Medals have gone to Ashkenazim as well as 37% of the Nobel Prizes in physics won by Americans.

    As for verbal IQ, I look forward to finding a suitable verbal threshold, but for now two-thirds of the puzzle is complete. In sum, from the frequency of appearance of Ashkenazic Jews in the annual USSR Chess Championships, we assess the mean Ashkenazic IQ to be 112. And from the frequency of Ashkenazic Fields medallists, we infer an Ashkenazic "math IQ" of 111. On these numbers, gentlemen, you can hang your yarmulkes.