Dogs, Runners and the Distribution of Human Attributes

With the beauty of Piemontese ladies still fresh upon his memory, whatever good intentions La Griffe might have entertained when he sat down at the keyboard to chronicle therewith the results of his recent musings, his attention was quickly diverted by thoughts of Piemonte in October, of white truffles in Alba and of the hounds that unearth them. From this improbable fusion of reverie and analysis emerged this account of biodiversity among dogs, runners and the tribes from whence they spring. Considered are such diverse questions as how gender differences in aggressiveness compare in men and dogs, and whether a European can ever again win an Olympic medal in distances over 1500m.

   In the northern province of Piemonte, about 100 km from the French border, the incomparable white truffle, il tartufo bianco d'Alba, grows wild beneath the surface of the soil. The grayish-amber fungus is sniffed out by dogs specially trained for this purpose. They are the Romagna Water Dogs or Truffle Hounds. By no means ordinary, these dogs are uniquely suited to the task of unearthing truffles, not only because of their splendid noses, but also because of their proficiency in the Piemontese dialect. Should you consider purchasing a truffle hound, tempted by the white truffle's price near $1300 a pound, be warned, your dog will not understand your commands even if you have good Italian. Be prepared to spend at least a year in Piemonte to learn its ancient dialect, unavailable in any school. Ancillary benefits of this experience will accrue, however, as Piemonte is the home of the Nebbiolo grape from which issue the aristocratic reds, Barolo and Barbaresco.

   Thousands of years of selective breeding have assured the dog's status as the most diverse species on earth. The curly-coated, robust Truffle Hound will never be confused with its diminutive effete cousin the Chihuahua. Linguistic deficiencies aside, the Chihuahua is not well suited to truffle foraging. His constitution and personality hinder him, not to mention olfactory shortcomings. Though few Chihuahuas could match the Romagna's unique gifts, a conscientious search within Chihuahuadom might reveal some specimens with a bit of promise. None would be ideal, but some would do better than others. A breeder, if so inclined, could begin with the best of these lap-loving runts and in time produce a dog of noble purpose.

   Nature, too, is a breeder. With time on her side, she has fashioned men into tribes, allotting each different portions of assorted endowments. And through adaptation, man has also acquired a degree of tribal heterogeneity. We focus, here, on one aspect of this heterogeneity: man's capacity to run long distances in short times. Though not as conspicuous as, say, the gap between Greyhound and Dachshund, the tribes of man display sufficient variability in this aptitude to produce profound differences in achievement. In this essay, we describe these variations in terms that allow us to predict the outcome of tribal competitions.

Tribal Variation in Running Ability
   Each of the more than thirty men who have run 100m in less than 10 seconds, can trace his ancestral roots to West Africa, but these same athletes, who wipe out everyone in distances below 400m, fail miserably at middle and longer distances. To find runners proficient at longer distances, we have only to cross Africa to the Great Rift Valley of western Kenya. There, between Lakes Rudolph and Victoria 6,000 to 8,000 ft above sea level, dwell the greatest distance runners the world has ever seen. A tiny bit of humanity, about 3.5 million strong, are as proficient above 800m as West Africans are in the sprints. John Manners, the eminent journalist and running authority, has dubbed them "the running tribe." Others know them simply as Kalenjin. One Kalenjin subtribe of a half million, from the Nandi district of the Rift Valley, produces more world-class endurance runners than Nations 500 times its size. Without exaggeration, Jon Entine, author of Taboo: Why Black Athletes Dominate Sports and Why We're Afraid to Talk About It, describes Nandis as "the greatest concentration of raw athletic talent in the history of sports."

   Tribal variation among runners has been well documented elsewhere, notably by John Manners and Jon Entine. Especially notable is a scholarly yet very accessible exposition by Vincent Sarich that puts running ability differences into a broad anthropological context (“The Final Taboo: Race Differences in Ability,” Skeptic, 8:1,38-43,2000). We shall not rehash these accounts. Instead, we pursue a decidedly Griffian line of attack. We shall compute the probability that a randomly selected European, trained to run 1500m, will do so faster than his Nandi counterpart, that a European will earn a medal in the men's 5000m in the Olympic Games of 2016, and much more. Finally, and most importantly, we shall develop algorithms that will enable the reader to play similar games of his own design.

The Measure of Man
   Height is easy to define, its distribution within a population easy to measure. We have no more to do than find a representative sample of adults and reach for a ruler. Other attributes may be more problematic. How, for example, do we determine a distribution of running ability within an entire population? Can we find a representative sample of tribesmen, provide each with motivation and training, and finally measure their times for some event? Not very likely. There is, however, a way out. In Aggressiveness, Criminality and Sex Drive by Race, Gender and Ethnicity, we introduced the method of thresholds. It applies nicely to this problem. The proportion of each tribe meeting or exceeding some threshold of performance is the only input it requires. When all is said and done, the precise definition of "ability" will still be fuzzy, a characteristic of the method of thresholds. That aside, we will have established running ability distributions in tribes relative to one another.

What is the probability that a randomly selected European, after appropriate training, will run 1500m faster than a similarly selected and trained Nandi?

   Some of the data we need are available from chroniclers of track and field. All-time-best lists are particularly useful. For a given event, such a list might contain 100, 500, 1500 or any number of the best times ever run. The slowest time on a list serves as the threshold of performance required by the method of thresholds. Each list includes every athlete in the world who has met or exceeded this standard.

   One of the most complete collections of all-time-best lists may be found on Peter Larsson's website, http://www.algonet.se/~pela2/. We use his 1500m all-time-best list to illustrate how the method of thresholds can quantify tribal differences in running ability. At this writing, Larsson's 1500m list contained the 899 best times ever recorded. His data go back to 1967, but we use only the 513 times recorded after Jan 1, 1996, so that we might compare contemporaneous athletes.

   Athletes may contribute more than once to an all-time-best list. In fact, the very best runners often contribute many times. Because the method of thresholds requires a list of best runners, not times, the list of 513 times is redundant. Removing the redundancy leaves a residue of 81 athletes, a roster of the world's best 1500m runners, each of whom had, in the past five years, contributed at least one all-time best performance. From this, using the method of thresholds, we can find mean ability differences at 1500m for all tribes represented on the best-runner list. Here's how.

   Suppose two groups A and B whose members display some property, x, which has a continuous range of values. (Standard units, SD, are used throughout.) Let P_A(x) and P_B(x) be the distributions of the property in groups A and B, respectively. The fractions, f_A and f_B, of each group with values of x greater than or equal to some threshold value, λ, are given by

   Suppose P_A(x) and P_B(x) differ only by a translation in x, such that f_B(x) = f_A(x - Δ), where Δ is the mean difference in x between the groups. Then the quantity, f_B, may be represented conveniently as

   For runners, the fractions, f_A and f_B, are computed relative to an appropriate part of a population. Thus for a men's event, women are excluded from the fraction denominator, as are the too young and the too old. Most of the eligible pool falls within an age range of approximately 15 years. Approximately 10 percent of many populations are men between the ages of 20 and 34. Thus for runners, we compute the fractions, f_A and f_B, by dividing the number of a tribe's athletes on a best-runner list by 10 percent of the tribe's population. CIA Factbook 2000 is a convenient source of population data.

Augmentation of Small Differences
   Near the limits of human performance, subtle differences between groups become greatly magnified. In world-class competition, whether for Nobel Prizes or Olympic gold, such small variations in group abilities profoundly influence tribal representation in the winner's circle. In "Black Athletes: Can Whites Measure up?," La Griffe du Lion, January 2000, we estimated the mean difference in sprinting ability between white and African Americans to be about 0.82 standard deviations. Despite this large group difference, if a white and black were selected randomly from their respective populations, the white would have almost a one in three chance of being the faster sprinter. Thus, a gap as big as 0.82 SD, which might go undetected in the ordinary scheme of life, is enough to create an all black elite at the top.

What is the probability that in the 2016 Olympics a person of European ancestry will win a medal in the men's 5000m? What is this probability for a Moroccan? For a Kalenjin? For a Kenyan irrespective of tribe?

   The augmentation effect is conveniently illustrated by comparing Western Europeans with Nandis in the men's 1500m. We took the combined populations of the UK, Germany and the Netherlands as representative of European aptitude. Each of these countries has a strong running program, and according to gene-frequency measurements, their native populations are closely related. (See, for example, "The History and Geography of Human Genes," Cavalli-Sforza et al, Princeton University Press, 1994.)

   Figure 1 displays 1500m ability distributions for Western European whites and Nandis. From the method of thresholds, we found a mean difference of 1.40 SD, the largest encountered in this study. Even so, the distributions overlap conspicuously. The "elite-runner threshold" shown in the figure is the minimum ability needed to make the 1500m best-runner list. But for a tiny few, the populations of both tribes fall below this threshold. Above it are the world's best runners.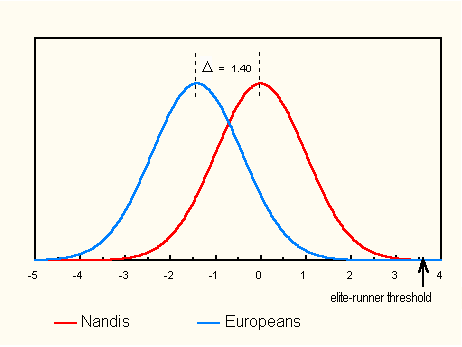

Figure 1.  Distributions of ability at 1500m for the Nandi and Western European tribes. Units are standard deviations. Europeans lag behind Nandis by 1.40 SD. The elite-runner threshold is the minimum ability needed to make the 1500m best-runner list.

   In Figure 2, we zoom in on the region beyond the threshold. There, represented by shaded areas under the curves, are the probabilities that a randomly selected young Nandi or European has the ability to make the 1500m best-runner list. A Nandi's chance of entering this select circle is so much greater than a European's, that we had to chop the top off the graph to make the area under the European curve big enough to see. The ratio of areas is 524:1. That is, a random Nandi is 524 times more likely to make the 1500m best-runner list than his West European counterpart!

   Even for a Nandi, the 1500m best-runner list is extremely select. The threshold it defines is 3.54 SD from the Nandi mean, 4.94 SD from the European mean. Only 1 in 5000 young Nandi men will be admitted to this exclusive circle. For Euros, the number is 1 in 2.6 million!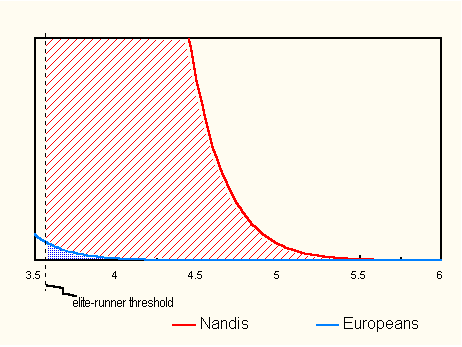

Figure 2.  Areas under the curves, beyond the "elite-runner threshold," are the probabilities that Nandi and European young men have what it takes to make the 1500m best-runner list. The ratio of areas is 524:1, meaning that a random Nandi is 524 times more likely to be in this elite group than a white European.

How the Tribes Stack up
   Table 1 lists relative running abilities for 12 tribes in 4 events, 1500m, 5000m, 10000m and the marathon. We define "relative running ability" of a tribe as the mean ability difference between it and the tribe of Europeans. The European entry in Table 1 is then zero for each event. The procedure is formally analogous to setting a zero of gravitational potential at some arbitrary height above sea level. The mean ability difference between any two tribes may be obtained by subtracting their table entries. The zero cancels. Data from 1995 through 2001 were used to produce best-runner lists for each event except 5000m, where 1994 data were included also to increase the size of the list.

Notes
• Larsson's lists, like most track and field compilations, include the nationality of athletes. Nationality and tribal origin, however, do not always coincide. This is more than occasionally true of "French" athletes who run under the Tricouleur, but have ancestral roots in former North African colonies. The middle distance runner, Driss Maazouzi, for example, is a French National, but Moroccan born. For our purposes, he is Moroccan.

• Kalenjin, whether Nandi or not, are the world's best distance runners. They outstrip every other tribe in every event. There is a big gap between Kalenjin at the top and everyone else. Thereafter, tribal differences decrease more gradually.

• In the four events we looked at, Non-Nandi Kalenjin are about as good as Nandis except at 1500m. There, Nandis outstrip other Kalenjin by 0.27 SD.

• Italian runners are marginally better than most other Western Europeans. Spaniards and Portuguese are decidedly better.

• John Manners graciously applied his encyclopedic knowledge of Kenyan runners to sort them out for us by tribe.

• The success of Europeans in international competition owes more to the size of their tribe than to their innate running ability.

• Portuguese, Spaniards, Moroccans, Algerians and non-Kalenjin Kenyans have comparable endurance running abilities.

• Serious marathoners can successfully compete in only two, perhaps three races a year. They may be tempted to run 10000m instead in order to improve their earnings. (Thanks to Steve Sailer for this insight.)

• Japanese are a significant force only in the marathon.

• Our focus is on aptitude. If a nation lacks either the commitment or resources needed to build a running program, its runners will be underrepresented on best-runner lists. In such cases our analysis will underestimate intrinsic ability. Burundians, for example, are extremely talented runners. They show up more than occasionally on best-runner lists, quite a feat for a country of 6 million. Still, their successes probably understate their talent. Burundians lack even the simplest amenities. In any given year, a Burundian will consume on average about 26 kilowatt-hours of electricity, enough to burn a 100 watt light bulb for about 11days. In the same year, a Moroccan will consume 440 kilowatt-hours, a Western European about 6,000 kilowatt-hours. Because Burundi numbers are depressed by circumstance, we cannot assess their true ability, and so we exclude them from this analysis.

General Problem 1.  More members of Group A can run, jump, think, etc., better than members of Group B. The mean ability difference between the groups is Δ (in standard units). Art belongs to group A, Bob to group B. That's all we know about Art and Bob. What is the probability, p(B > A), that Bob can run, jump, think or whatever better than Art?

Solution:  Let P_A(x)dx be the probability that Art's ability lies between x and x + dx. Let P_B(x)dx be the corresponding probability for Bob. The probability that Bob's ability exceeds x is

   The simultaneous probability that Art's ability is between x and x + dx, and that Bob's ability exceeds Art's, is

   The probability, p(B > A), that Bob can outperform Art is the probability (5) integrated over all x. That is,

   Given a mean difference, Δ, between two groups, (7) gives the probability that a member of the less able group (B) will outperform a member of the more able group (A) when both are selected randomly.

   Here is a specific application of (7).

What is the probability that a randomly selected European, after appropriate training, will run 1500m faster than a similarly selected and trained Nandi?

   From Table 1, we find the Nandi-European mean difference to be 1.40 SD. Assuming Gaussian distributions, (7) yields 0.16 for this probability. That is, a European has a 16 percent chance of beating a Nandi at 1500m.

   For the reader who finds it inconvenient to perform this and similar calculations, we provide a graph of the function p(B > A). It is displayed in Figure 3, and may be applied to any property for which a group mean difference, Δ, is known. The graph of Figure 3 gives the probability that a randomly selected member of a less able group will outperform a randomly selected member of a more able group. Application of (7) is not confined to matters of sport. It applies equally well in realms far removed from track and field.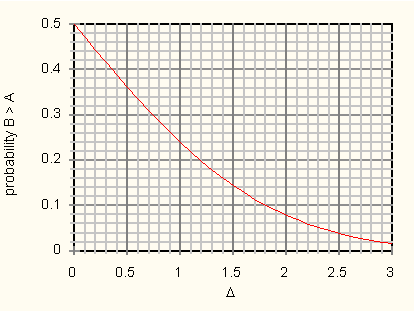

Figure 3.  If Group B lags behind Group A in some property by Δ standard deviations, the function p(B > A) gives the probability that a random member of the less able group will outperform a random member of the more able group.

   Values for group mean differences are scattered throughout this website. In Aggressiveness, Criminality and Sex Drive by Race, Gender and Ethnicity, for example, we estimated the male-female "aggressiveness" difference to be 0.65 SD. Figure 3 helps us to interpret the 0.65 SD difference. From the graph, we see that a random selection of a man and a woman will find the woman more aggressive 32 percent of the time. In the ordinary affairs of man such a difference could be easily overlooked, but at extreme levels of aggressive behavior, say that which triggers violent criminal conduct, a difference of 0.65 SD is telling. The low rate of female criminal violence (relative to male) is but another illustration of the effect in which group differences become amplified in the tails of a distribution.

General Problem 2.  Members of various groups vie for a limited number of slots, the slots to be filled in rank order of ability. From known mean ability differences, find the number from each group that secure slots.

Solution: Let the ability, x, be distributed among the members of group i in accordance with the normalized distribution function, P_i(x). Let λ be the minimum ability (in standard units) needed to secure a slot, i.e., the ability of the least able slot holder. If Group i has N_i members, the number, n_i, of its members who fill slots is given by:

   If N_S is the number of slots, then the following relation will be satisfied:

In (9) the sum is over all groups.

   Suppose the distribution functions for the various groups differ from one another by a translation in x, but are otherwise identical. Let P(x) be the distribution function of some hypothetical reference group. Then the distribution function for the i^th group may be written:

   The transformation (3) applied to (11) yields the expression:

   One of the groups, say Group k, may be taken as the reference group, in which case Δ_k = 0. The i^th term on the right-hand side of (12) gives the number of Group i members that earn slots.

   To implement (12) we need values for the Δ's. Sometimes they are known from direct measurement, but usually they are not. Most often we obtain them from the method of thresholds.

Suppose in the year 2024 all the world's men of an age characteristic of world-class distance runners are assembled to compete against each other in a 5000m race. Each has trained to the best of his ability. What will be the tribal affiliations of the first 100 to finish?

   The reader may wonder why we begin with an event so many years down the road. It is because we know too much about the present and immediate future. To make a prediction about an imminent event, there is no substitute for being on the ground, observing the field of competitors, learning their strengths and weaknesses. Consider, for example, the recent Olympic Games in Sydney. It was a pretty safe bet, coming into the Games, that a Moroccan would be among the men's 1500m medalists, not because Moroccans dominate this event, but rather because Hicham El Guerrouj was in the field. The Moroccan miler had not lost at 1500m in four years since the previous Games in Atlanta, where he tripped and came in dead last. (Ironically, he was beaten in Sydney by a Nandi, Noah Ngeny, and had to settle for silver. Thus, El Guerrouj had the questionable distinction of losing at 1500m in two successive Olympics, while winning every race in between.)

   Our analysis can accommodate the El Guerroujs of the world. It does not know when or where they will appear, but it does know which tribes are likely to produce them. In a circle of 100 best runners, the El Guerrouj effect is not much of an issue. El Guerrouj clones will be lost in the numbers. Equation (12) can, with reasonable accuracy, determine the tribal identities of the 100. Using N's from population data, Δ's from the method of thresholds, and with the number of slots, N_S, set to 100, (12) yields λ, the minimum ability required to make the circle of 100. With this value of λ, each term of (12) may be evaluated to give the number from each tribe predicted to be among the world's 100 best.

   In our analysis, we included Kalenjin, other Kenyans, Moroccans, Spaniards, Ethiopians, and Western Europeans. The remaining tribes of the world were lumped into one super tribe: "Others." We included in Others only tribes that had demonstrated some success at distance running. Algeria, Burundi, Brazil, Czech Republic, Japan, Mexico, Romania, Rwanda, Slovakia, Somalia, South Africa, Sudan, Tunisia, and Ukraine with a combined population of about 630 million were the constituent tribes of Others. The mean ability difference between Europeans and Others at 5000m was determined by the method of thresholds to be -0.13 SD. That is, Others lagged behind Europeans by 0.13 SD.

   Table 2 gives the tribal breakdown of the world's 100 best 5000m runners as predicted by (12). Note how Kalenjin, only 3.5 million of the world's 6-billion-plus, are predicted to make up 27.9 percent of the top hundred.

   Table 2 also shows the expected tribal representation when the number of slots, N_S, is narrowed to 3 (the number of Olympic medalists). The representation of Kalenjin increases dramatically to 41.3 percent at the expense of the less talented tribes. Except for Moroccans, whose representation remains approximately constant, the other tribes suffer significant losses. The order for "Others" and Spaniards is actually reversed, demonstrating the extreme nonlinearity of this problem.

What is the probability that in the 2016 Olympic Games a person of European ancestry will win a medal in the men's 5000m? What is this probability for a Moroccan? For a Kalenjin? For a Kenyan irrespective of tribe?

   The probability that a West European will medal in this event may be taken as the predicted West European fraction among the medalists. Table 2 gives this probability as 0.092 for Europeans, 0.162 for Moroccans, and 0.413 for Kalenjin. For Kenyans irrespective of tribe, the probability is the sum of the Kalenjin and non-Kalenjin Kenyan probabilities, or 0.542. Kenyans are the only competitors with a better than even chance of medaling in the men's 5000m run at the 2016 Olympic Games.

   The small number of medals, i.e., 3, awarded in each event is a situation not very accommodating to oracles, so we consider also 7 successive Olympic Games, boosting the number of medals awarded in this event to 21.

In the 7 Olympic Games to be held between 2016 and 2040, what is the probability that a person of European ancestry will win at least one of the 21 medals to be awarded in the men's 5000m? What about Moroccans, Kalenjin and Kenyans irrespective of tribe?

   We have seen that the probability of a European winning a 5000m medal in 2016 is 0.092. In 7 Games, the probability that no European medals is then (1 - 0.092)⁷. And, the probability that at least one European medals is 1 - (1 - 0.092)⁷, or 0.51. Thus, Europeans have a slightly better than 50 percent chance of garnering at least one medal in the men's 5000m over a 7 Olympic-Game stretch. Similar calculations yield probabilities of 70.9% for Moroccans, 97.6% for Kalenjin, and 99.6% for Kenyans irrespective of tribe. It is a virtual certainty that a Kenyan will win at least one of the 21 medals for 5000m to be awarded over the course of 7 Olympics.

Aggressiveness in Man and Dog
   We conclude as we began -- with the dog. Like his master, he occasionally crosses the line that separates the permissible from the forbidden. Each year in the United States, 585,000 dog-bite injuries require medical attention. (Sosin et al, Accid Anal Prev. 24, 685, 1992.) Gershman et al, in Pediatrics, 93 No. 6, 913, 1994 report that male dogs do most of the biting, being 6.2 times more likely to bite than females. These data and the estimate of 53 million dogs in the US, provide all the ingredients necessary to find the canine male/female aggressiveness difference. Using biting as a threshold for aggressiveness, the method of thresholds provides the key. The result is remarkable.

   If half the dogs are male, and we assume one bite per dog, 1.90% of males and 0.307% of females are biters. Allowing for repeat offenders, suppose the number of biters is 70 percent of the number of bites. Then, 1.33% of males and 0.215% of females are biters. The two assumptions establish a range of input to the method of thresholds. The output yields a canine male/female mean aggressiveness difference between 0.64 and 0.67 SD. Recalling the man/woman aggressiveness difference of 0.65 SD, we are reminded of the many ways in which man and dog are alike, and man and woman are unalike.

# # #